Home /
Expert Answers /
Algebra /
matrix-a-is-factored-in-the-form-pdp-1-use-the-diagonalization-theorem-to-find-the-eigenvalues-pa812
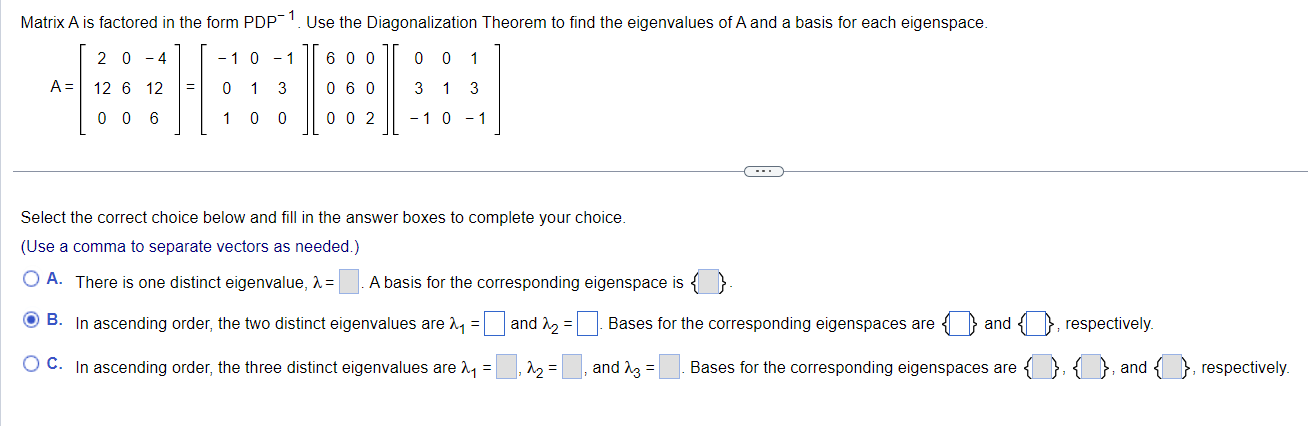
(Solved): Matrix A is factored in the form PDP^(-1). Use the Diagonalization Theorem to find the eigenvalues ...
Matrix
Ais factored in the form
PDP^(-1). Use the Diagonalization Theorem to find the eigenvalues of
Aand a basis for each eigenspace.
A=[[2,0,-4],[12,6,12],[0,0,6]]=[[-1,0,-1],[0,1,3],[1,0,0]][[6,0,0],[0,6,0],[0,0,2]][[0,0,1],[3,1,3],[-1,0,-1]]Select the correct choice below and fill in the answer boxes to complete your choice. (Use a comma to separate vectors as needed.) A. There is one distinct eigenvalue,
\lambda =A basis for the corresponding eigenspace is . B. In ascending order, the two distinct eigenvalues are
\lambda _(1)=and
\lambda _(2)=. Bases for the corresponding eigenspaces are {} and {} , respectively. C. In ascending order, the three distinct eigenvalues are
\lambda _(1)=,\lambda _(2)=, and
\lambda _(3)=. Bases for the corresponding eigenspaces are
