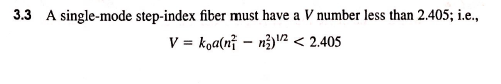(Solved):   3.3 A single-mode step-index fiber must have a \( V \) number less than \( 2.405 \); i.e ...

 

3.3 A single-mode step-index fiber must have a \( V \) number less than \( 2.405 \); i.e., \[ V=k_{0} a\left(n_{1}^{2}-n_{2}^{2}\right)^{1 / 2}<2.405 \] a. Show that the expression derived in Problem 3.1(b) \( \left(N \simeq 4 V^{2} / \pi^{2}\right) \) still applies, provided we realize that a single-mode fiber supports two independently polarized \( \mathrm{HE}_{11} \) modes (or \( \mathrm{LP}_{01} \) modes). b. With \( a=5 \mu \mathrm{m}, n_{2}=1.50 \), and \( \lambda=1 \mu \mathrm{m} \), find the maximum core index for a single-mode fiber. (Answer: \( n_{1}=1.50195 \).) c. With \( n_{1}=1.501, n_{2}=1.500 \), and \( \lambda=1 \mu \mathrm{m} \), find the maximum core radius \( \mathrm{f}_{0 \mathrm{r}} \) a single-mode fiber. (Answer: \( a=7 \mu \mathrm{m} \).) d. Show that the confinement factor for a single-mode fiber is \[ \Gamma_{1}=\frac{P_{\text {core }}}{P}=\frac{(q a)^{2}}{V^{2}}\left(1+\frac{J_{0}^{2}(h a)}{J_{1}(h a)}\right) \] where \( h a \) satisfies the mode condition (3.3-26) \[ h a \frac{J_{1}(h a)}{J_{0}(h a)}=q a \frac{K_{1}(q a)}{K_{0}(q a)} \] e. Show that, by using the table of Bessel functions, \( h a=1.647 \) is an approximate solution to the mode condition for \( V=2.405 \). Evaluate the confinement factor \( \Gamma_{1} \) for the \( \mathrm{LP}_{01} \) mode of this single-mode fiber (Answer: \( \Gamma_{1}=83 \% \) ). Note that this is the maximum confinement factor for a single-mode fiber. Compare this value with the curves in Figure 3-9.