(Solved): Not so simple Graph Problem Statement Write C++ code for implementing a Graph data structure that s ...

Not so simple Graph Problem Statement Write C++ code for implementing a Graph data structure that supports a directed graph with self-loops and paralel edges. You are erpected to implement the following methods and a main method is already built for you: void insertEdge int from, int to. int weightt: bodl is Edge(int from, int to): int sumEdge(int from, int to): vectorcints gef Weight [int from, int to\}; vectorkint> getAdjacent(int vertex): Explanation - insortedge() adds a new edge between the from and to vertex. - isEdge() returns a boolean indicating true if there is an edge between the from and to vertex. - sumEdge0 returns the sum of weights of all odges connecting the from and fo vertex: Returns 0 if no edges connect the two vertices. - getweight(1) teturns a sorted vector containing all weights of the edges connecting the from and to vertex. - getA?djacent0 returns a sorted vector of all vertices that are connected to a verter. Note that the values can be duplicates. Sample input \[ \begin{array}{llll} 7 & & & \\ 1 & 0 & 6 & 1 \\ 1 & 0 & 1 & 20 \\ 1 & 0 & 2 & 30 \\ 2 & 0 & 0 \\ 3 & 0 & 2 \\ 4 & 0 & 1 \\ 5 & 0 \end{array} \] Sample Output \[ \begin{array}{l} 1 \\ 38 \\ 20 \\ 8.12 \end{array} \] Explanation - Input: Line 1 denotes the number of lines (n) that follow. Each nect line denctes a call to one of the five functicns you noed to impiement. The first leter of every ine denctes getweight?) 5 is pet ddiacentu. This is followed with the necess ry porameters. - Output: Output is the printing of returned values from respectiof function calfs that retuin some yalue and are not of void return type. 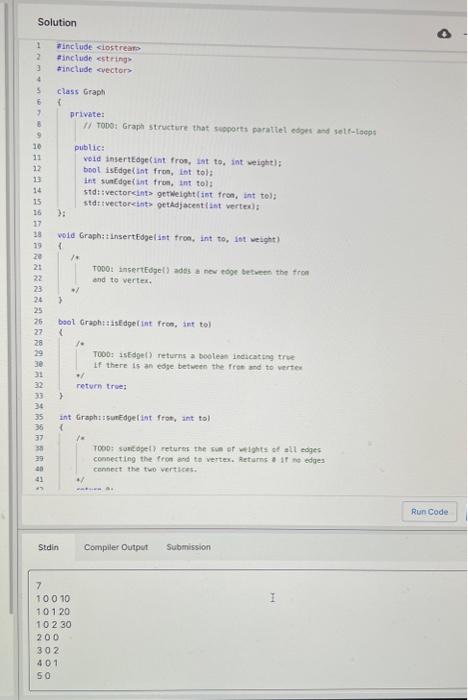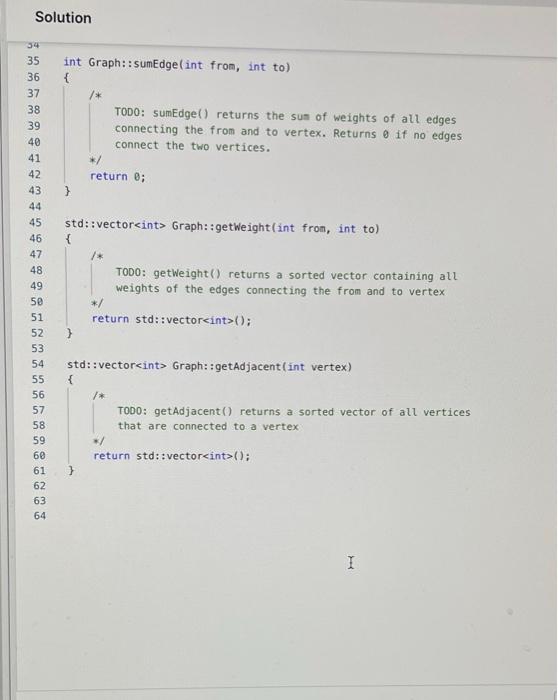Solution Solution