Home /
Expert Answers /
Statistics and Probability /
p-values-formulas-homework-due-jul-9-2025-07-59-edt-in-each-of-the-following-questions-you-are-giv-pa381
(Solved): P-Values Formulas Homework due Jul 9, 2025 07:59 EDT In each of the following questions, you are giv ...
P-Values Formulas
Homework due Jul 9, 2025 07:59 EDT
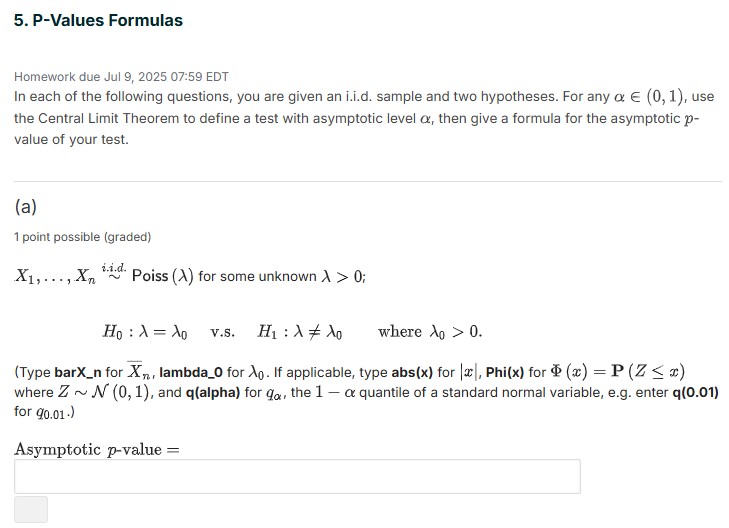
In each of the following questions, you are given an i.i.d. sample and two hypotheses. For any \alpha in(0,1), use
the Central Limit Theorem to define a test with asymptotic level \alpha , then give a formula for the asymptotic p -
value of your test.
(a)
1 point possible (graded)
x_(1),dots,x_(n)?^( i.i.d. ) Poiss (\lambda ) for some unknown \lambda >0;
H_(0):\lambda =\lambda _(0), v.s. ,H_(1):\lambda !=\lambda _(0), where \lambda _(0)>0.\bar{x} _(n), lambda_(0) for \lambda _(0). If applicable, type abs(x) for |x|, Phi(x) for \Phi (x)=P(Z<=x)
where Z?N(0,1), and alpha