(Solved): Part A - Finding the Cartesian components of a force described by direction angles Learning Goal: ...

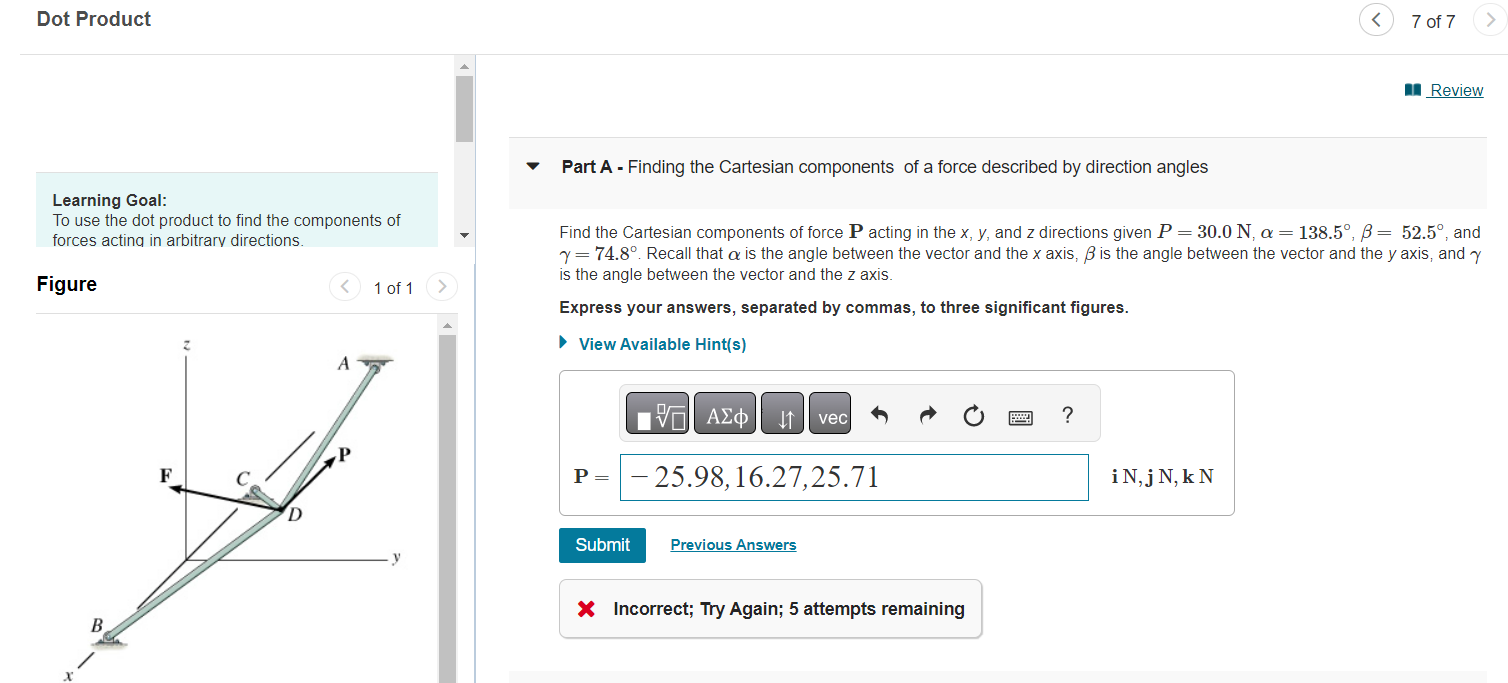
Part A - Finding the Cartesian components of a force described by direction angles Learning Goal: To use the dot product to find the components of forces actina in arbitrary directions. Find the Cartesian components of force \( \mathbf{P} \) acting in the \( x, y \), and \( z \) directions given \( P=30.0 \mathrm{~N}, \alpha=138.5^{\circ}, \beta=52.5^{\circ} \), and \( \gamma=74.8^{\circ} \). Recall that \( \alpha \) is the angle between the vector and the \( x \) axis, \( \beta \) is the angle between the vector and the \( y \) axis, and \( \gamma \) Figure is the angle between the vector and the \( z \) axis. Express your answers, separated by commas, to three significant figures. 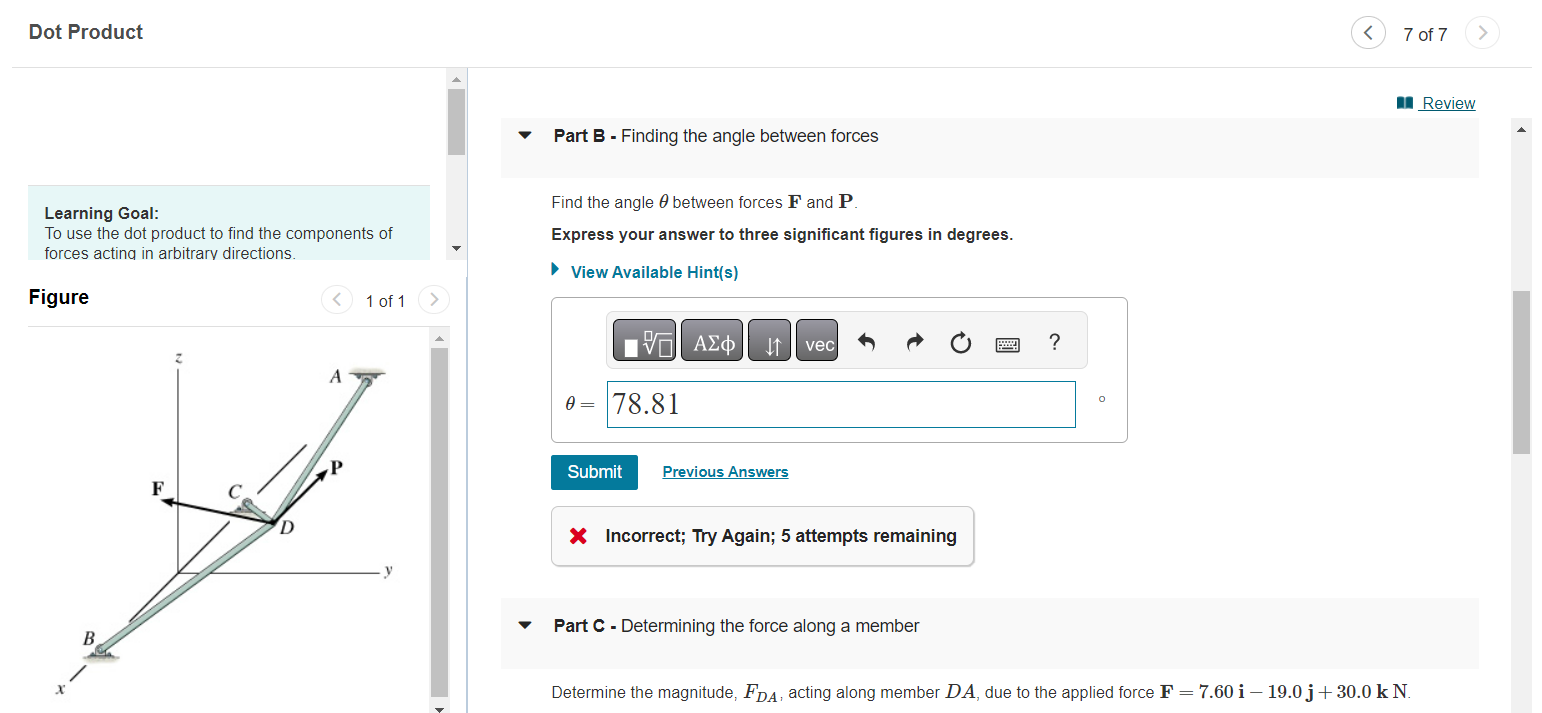\( X \) Incorrect; Try Again; 5 attempts remaining Dot Product 7 of 7 Part B - Finding the angle between forces Learning Goal: Find the angle \( \theta \) between forces \( \mathbf{F} \) and \( \mathbf{P} \). To use the dot product to find the components of Express your answer to three significant figures in degrees. forces acting in arbitrary directions. Figure 1 of 1 \( \theta= \) \( x \) Incorrect; Try Again; 5 attempts remaining Part C - Determining the force along a member Determine the magnitude, \( F_{D A} \), acting along member \( D A \), due to the applied force \( \mathbf{F}=7.60 \mathbf{i}-19.0 \mathbf{j}+30.0 \mathbf{k} \mathrm{N} \). 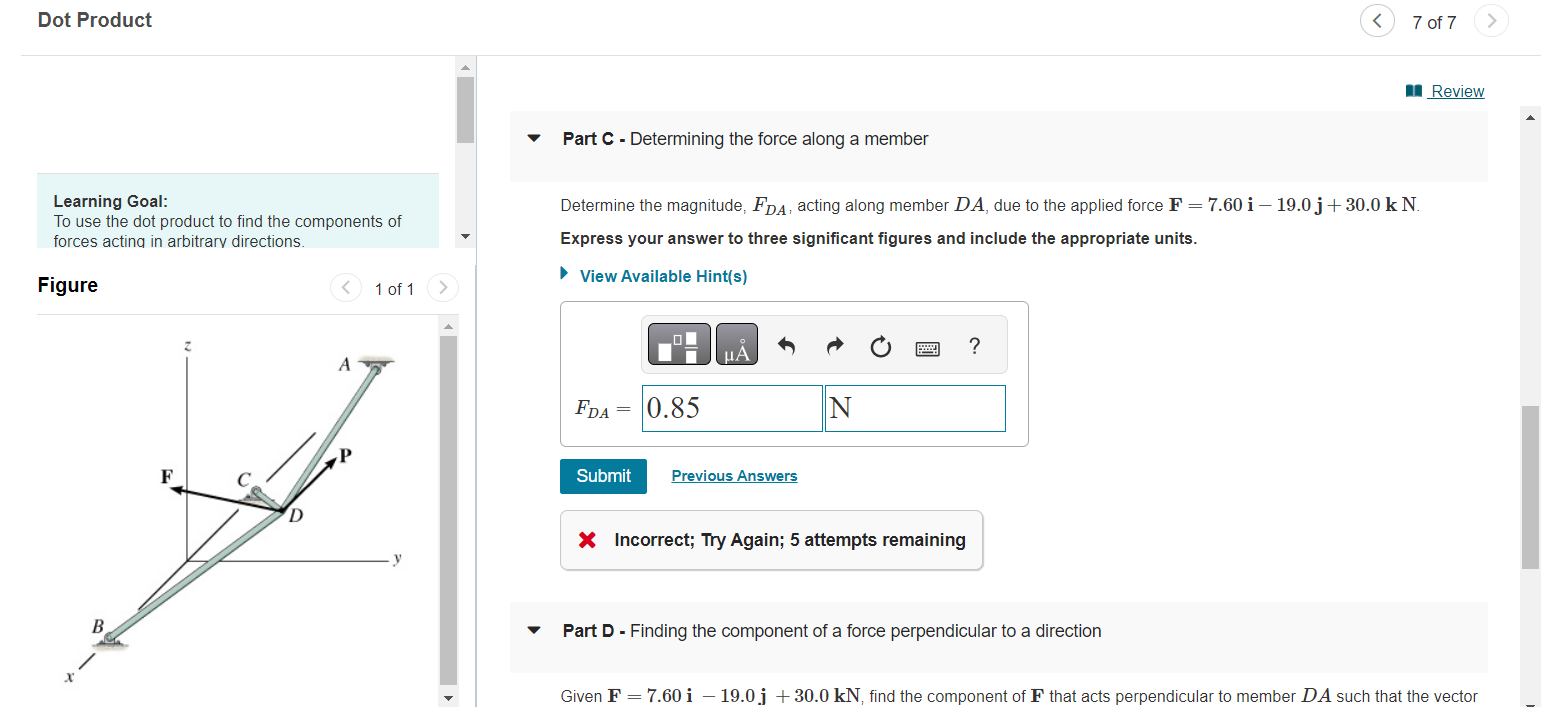Dot Product 7 of Part C - Determining the force along a member Learning Goal: To use the dot product to find the components of Determine the magnitude, \( F_{D A} \), acting along member \( D A \), due to the applied force \( \mathbf{F}=7.60 \mathbf{i}-19.0 \mathbf{j}+30.0 \mathbf{k} \mathrm{N} \). forces acting in arbitrary directions. Express your answer to three significant figures and include the appropriate units. 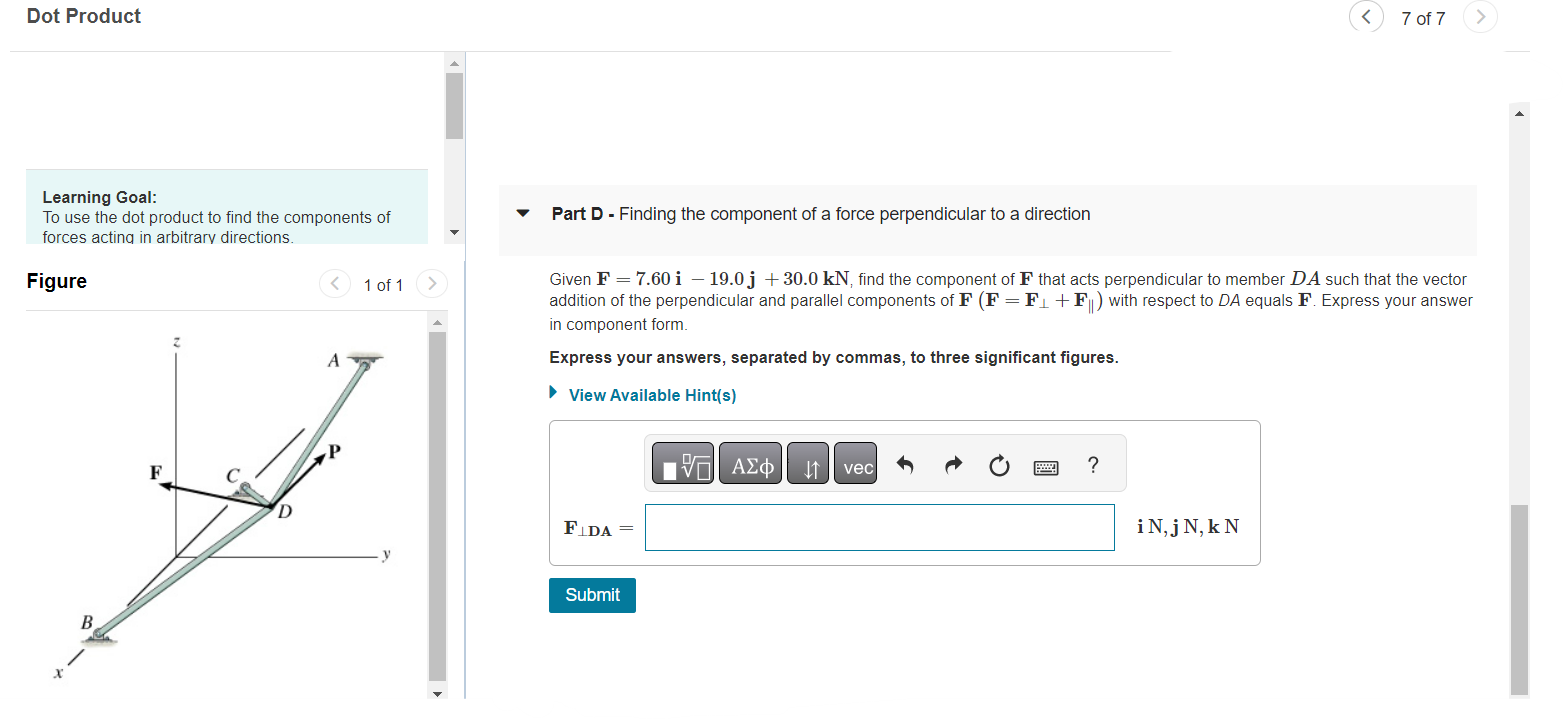Figure 1 of 1 \( X \) Incorrect; Try Again; 5 attempts remaining Part D - Finding the component of a force perpendicular to a direction Given \( \mathbf{F}=7.60 \mathbf{i}-19.0 \mathbf{j}+30.0 \mathrm{kN} \), find the component of \( \mathbf{F} \) that acts perpendicular to member \( D A \) such that the \( \mathrm{v} \) Dot Product 7 of 7 Learning Goal: To use the dot product to find the components of Part D - Finding the component of a force perpendicular to a direction forces acting in arbitrary directions. Figure Given \( \mathbf{F}=7.60 \mathbf{i}-19.0 \mathbf{j}+30.0 \mathbf{k N} \), find the component of \( \mathbf{F} \) that acts perpendicular to member \( D A \) such that the vector addition of the perpendicular and parallel components of \( \mathbf{F}\left(\mathbf{F}=\mathbf{F}_{\perp}+\mathbf{F}_{\|}\right) \)with respect to \( D A \) equals \( \mathbf{F} \). Express your answer in component form. Express your answers, separated by commas, to three significant figures.