(Solved): Please help answer the table and draw the Fnet line on the graph wirh correct angle according to the ...

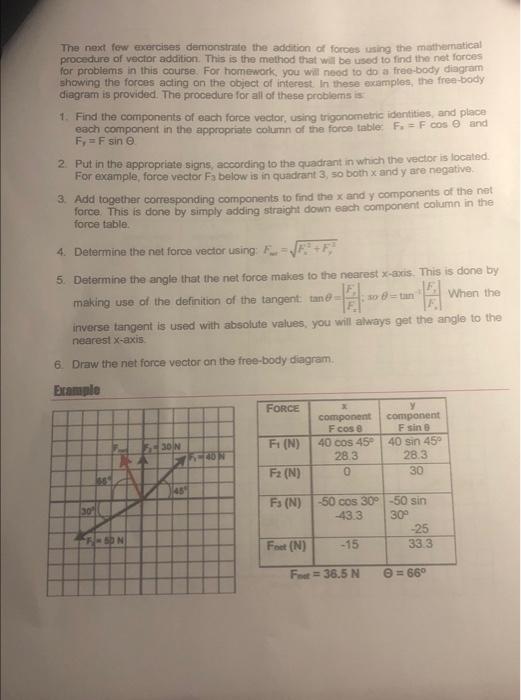
The next fow exercises demonsdrate the addition of forces using the mathermatical procedure of vector addition. This is the method that will be used to find the net forces for problems in this course. For homework, you will neod to dn a free-body diagram showing the forces acling on the object of interest. In these examples, the freebody diagram is provided. The procedure for all of these problems a 1. Find the components of aach force vector, using trigornometric isontibes, and place each component in the appropriate column of the force table; \( F_{x}=F \cos Q \) and \( F_{r}=F \sin \theta \) 2 Put in the appropriate signs, according to the quadrant in whech the vector is localed. For example, force vector Fa below is in quadrant 3, so both \( x \) and \( y \) are negative. 3. Add together corresponding components to find the \( x \) and y components of the net force. This is done by simply adding straight down each component colurnn in the force table. 4. Determine the net force vector using: \( F_{m}=\sqrt{F_{w}^{3}+F_{y}^{1}} \) 5. Determine the angle that the net force makes to the nearest \( x \)-axis. This is done by making vse of the definition of the tangent: \( \tan \theta=\left|\frac{F}{F_{2}} ; \sin \theta=\tan \right| \frac{F_{k}}{F_{\text {. }}} \mid \) When the inverse tangent is used with absolute values, you will ahways get the angle to the nearest \( x \)-axis. 6. Draw the net force vector on the free-body diagram. 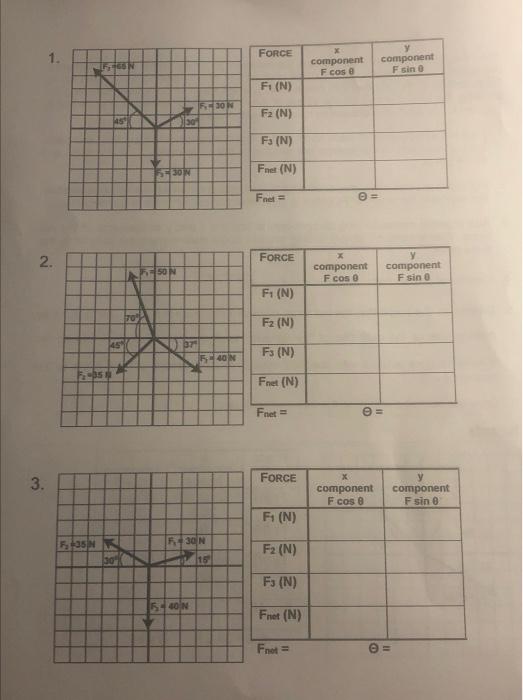1. \begin{tabular}{|l|c|c|} \hline Force & \( x \) component F cos \( \theta \) & component \( F_{\sin \theta} \theta \) \\ \hline\( F_{1}(\mathrm{~N}) \) & & \\ \hline\( F_{2}(N) \) & & \\ \hline\( F_{3}(\mathrm{~N}) \) & & \\ \hline\( F_{\text {net }}(\mathrm{N}) \) & \\ \hline\( F_{n e t}= \) & \( \Theta= \) \\ \hline \end{tabular} 2. \begin{tabular}{|l|c|c|} \hline FORCE & \( \mathrm{x} \) component \( \mathrm{F} \cos \theta \) & y component \( \mathrm{F} \sin \theta \) \\ \hline\( F_{1}(\mathrm{~N}) \) & & \\ \hline\( F_{2}(\mathrm{~N}) \) & & \\ \hline\( F_{3}(\mathrm{~N}) \) & & \\ \hline Fnet (N) & \\ \hline Fnet \( = \) & \( \Theta= \) \\ \hline \end{tabular} 3.