Home /
Expert Answers /
Advanced Math /
please-kindly-explain-and-show-works-thank-you-12-a-find-the-area-enclosed-by-one-loop-the-polar-pa581
(Solved): Please kindly explain and show works. Thank you! 12. a) Find the area enclosed by one loop the polar ...
Please kindly explain and show works. Thank you!
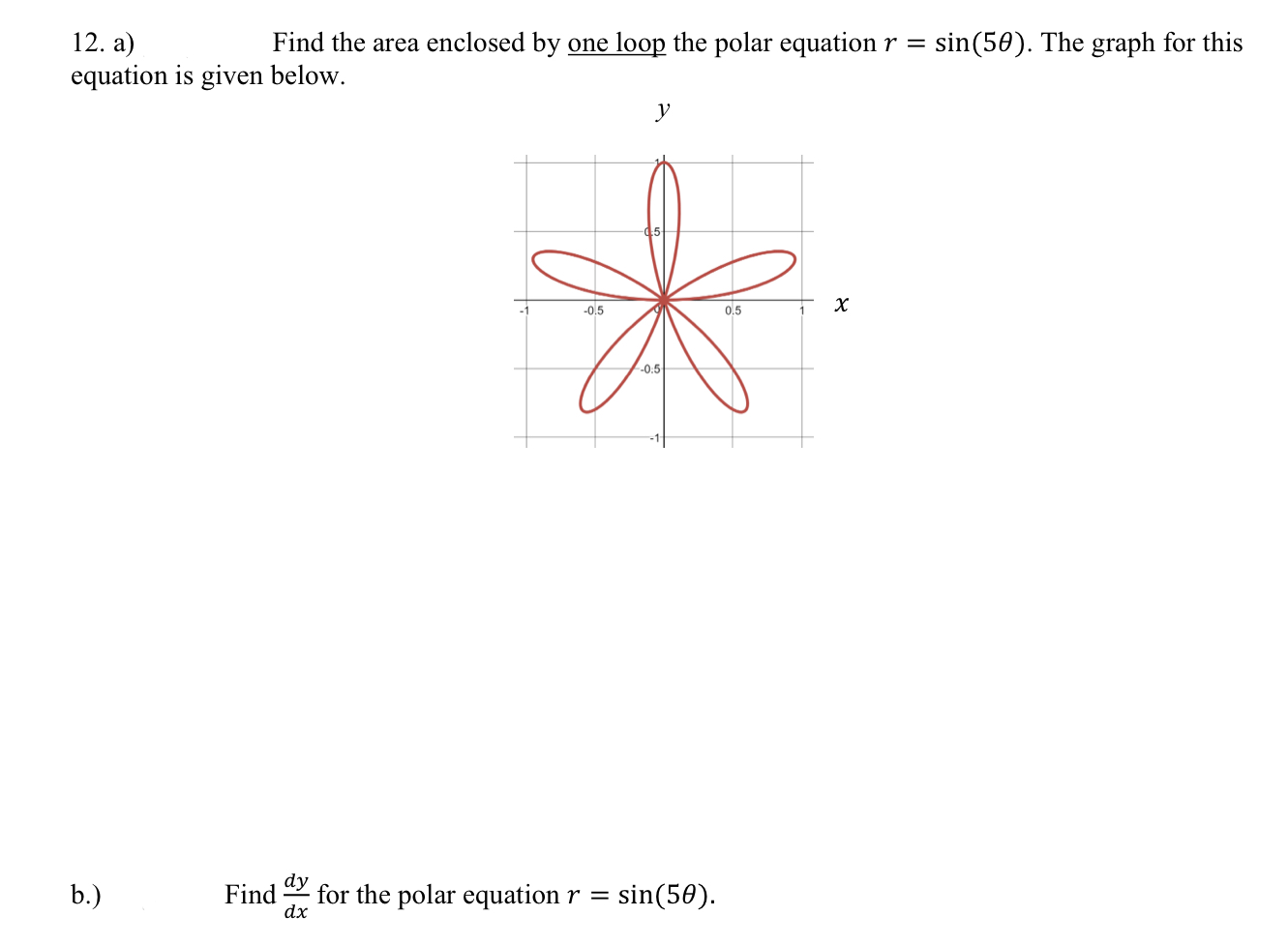


12. a) Find the area enclosed by one loop the polar equation . The graph for this equation is given below. b.) Find for the polar equation .
11. Consider the curve defined by the parametric equations below: Find the point(s) where the curve has a vertical tangent line. Set up, but do not evaluate, a definite integral representing the exact length of the curve.
10. Find a Taylor series for the function below. Express your answer in summation notation and simplity completely within the summation. Centered at
Expert Answer
12. a) To find the area enclosed by one loop of the polar equation r = sin(50), we need to evaluate the integral of (1/2)r^2 w.r.t theta from theta = 0 to theta = 2?. The integral represents the area enclosed by the curve.b) To find dy/dx for the polar equation r = sin(50), we can use the chain rule. We can express the polar equation in Cartesian form and then differentiate y with respect to x.a) To find the area enclosed by one loop of the polar equation r = sin(50), we need to evaluate the integral of (1/2)r^2 with respect to theta from theta = 0 to theta = 2?. Here's the step-by-step solution:The equation r = sin(50) represents a curve in polar coordinates. To find the area enclosed by one loop, we can evaluate the integral:Area = (1/2) (r^2) d?Substituting the given value of r = sin(50), we have:Area = (1/2) ?[0 to 2?] (sin^2(50)) d?We can use the trigonometric identity sin^2(?) = (1/2)(1 - cos(2?)) to simplify the integral:Area = (1/4) ?[0 to 2?] (1 - cos(100?)) d?Integrating term by term, we get:Area = (1/4) [? - (1/100)sin(100?)] evaluated from ? = 0 to ? = 2?Evaluating the limits, we have:Area = (1/4) [(2? - (1/100)sin(200?)) - (0 - (1/100)sin(0))]Since sin(0) = 0 and sin(200?) = 0, we have:Area = (1/4) (2? - 0) = ?/2Therefore, the area enclosed by one loop of the polar equation r = sin(50) is ?/2.b) To find dy/dx for the polar equation r = sin(50), we can use the chain rule. We can express the polar equation in Cartesian form and then differentiate y with respect to x.The Cartesian form of the polar equation r = sin(50) is:x = r cos(?) = sin(50) cos(?) y = r sin(?) = sin(50) sin(?)Taking the derivative of y with respect to x:dy/dx = (dy/d?) / (dx/d?)To find dy/d?, we can differentiate y = sin(50) sin(?) with respect to ?:dy/d? = sin(50) cos(?)To find dx/d?, we can differentiate x = sin(50) cos(?) with respect to ?:dx/d? = -sin(50) sin(?)Now, we can substitute these values into the derivative dy/dx:dy/dx = (sin(50) cos(?)) / (-sin(50) sin(?))The sin(50) terms cancel out:dy/dx = -cot(?)Therefore, the derivative dy/dx for the polar equation r = sin(50) is -cot(?).