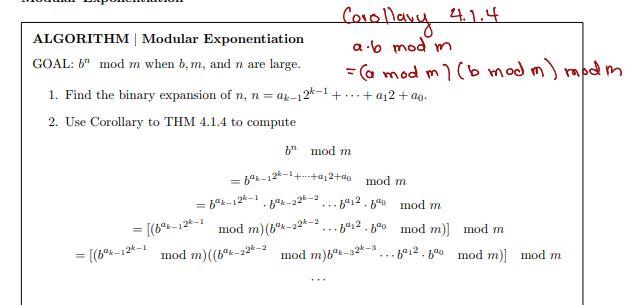(Solved): PLEASE USE THE ALGORITHM AND PSEUDOCODE EXAMPLE PROVIDED. PLEASE CODE IN PYTHON USING JUPYTER!!! ...

PLEASE USE THE ALGORITHM AND PSEUDOCODE EXAMPLE PROVIDED.

PLEASE CODE IN PYTHON USING JUPYTER!!! THANKS

Program a function mod_exp $$(b,n,m)$$ that computes $$b^n\mathrm{mod}m$$ using the algorithm discussed in lecture. No credit will be given to functions that employ any other implementation. For example, if the function implementation simply consists of $$b??n\%m$$, no credit will be given. The function should satisfy the following: 1. INPUT: - $$b$$ - positive integer representing the base - $$n$$-positive integer representing the exponent - $$m$$ - positive integer representing the modulo 2. OUTPUT: - the computation of $$b^n\mathrm{mod}m$$ if $$b,n,m$$ are positive integers, 0 otherwise. EXAMPLE: \mod_exp $$(3,644,645)$$ 36 Corollavy $$\mathrm{4.1.4}$$ ALGORITHM | Modular Exponentiation $$a.6\mathrm{mod}m$$ GOAL: $$b^n\mathrm{mod}m$$ when $$b,m$$, and $$n$$ are large. $$=(a\mathrm{mod}m)(b\mathrm{mod}m)\mathrm{mod}m$$ 1. Find the binary expansion of $$n,n=a_{k?1}{2}^{k?1}+?+a_{1}2+a_0$$. 2. Use Corollary to THM 4.1.4 to compute $$\begin{array}{l}{b}^n\mathrm{mod}m\\ =b^{a_{k?1}{2}^{k?1}}?b^{a_{k?2}{2}^{k?2}}?b^{a_{1}2}?b^{a_0}\mathrm{mod}m\\ =\left[\left(b^{a_{k?1}{2}^{k?1}}\mathrm{mod}m\right)\left(b^{a_{k?2}{2}^{k?2}}?b^{a_{1}2}?b^{a_0}\mathrm{mod}m\right)\right]\mathrm{mod}m\\ =\left[\left(b^{a_{k?1}{2}^{k?1}}\mathrm{mod}m\right)\left(\left(b^{a_{k?2}{2}^{k?2}}\mathrm{mod}m\right)b^{a_{k?3}{2}^{k?3}}?b^{a_{1}2}?b^{a_0}\mathrm{mod}m\right)\right]\mathrm{mod}m\end{array}$$ PSEUDOCODE | Modular Exponentiation INPUT: $$b$$-integer, $$m$$-integer, $$n={\left(a_{k?1},a_{k?2},\dots ,a_1,a_0\right)}_2$$ OUTPUT: $$b^n\mathrm{mod}m$$