(Solved): Problem 1 (30 points). Consider the PUMA robot depicted in Figure 1, where the DH coordinate frames ...

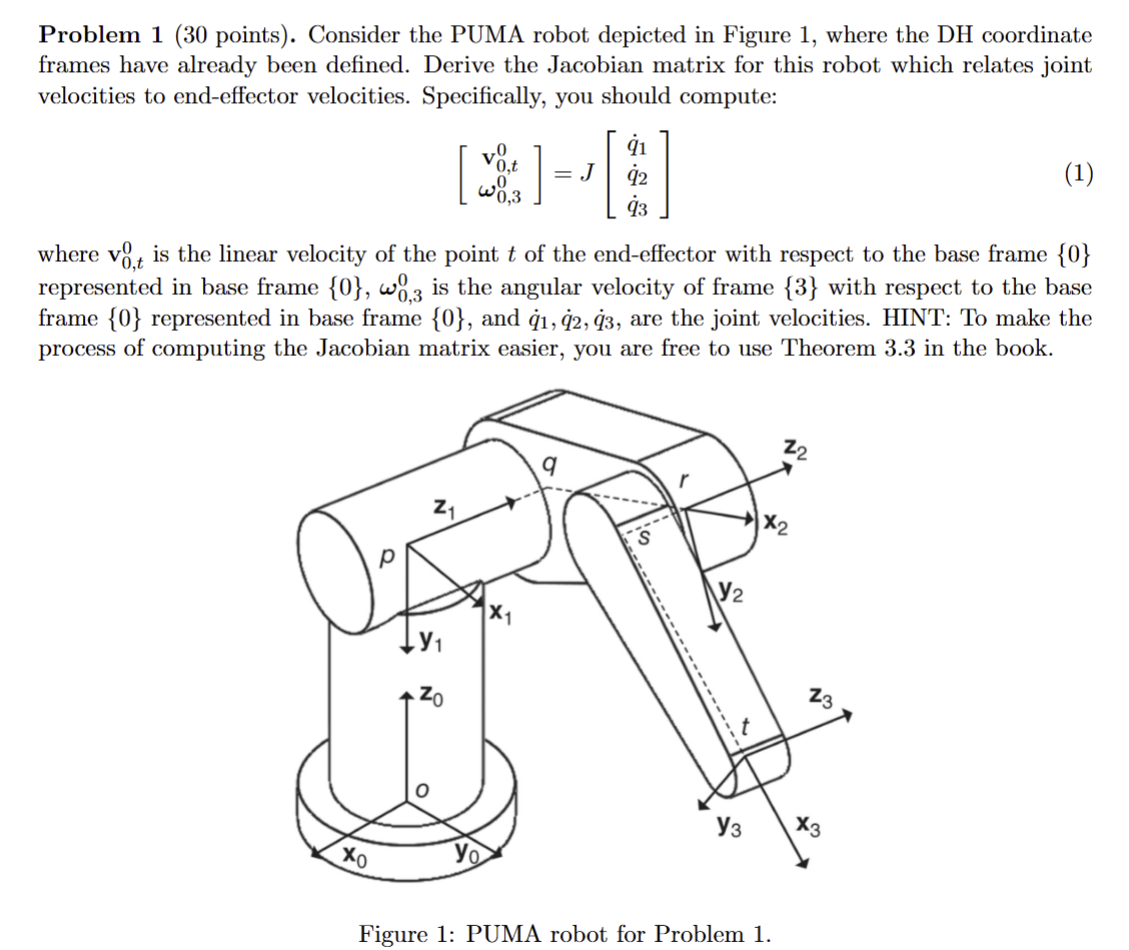
Problem 1 (30 points). Consider the PUMA robot depicted in Figure 1, where the DH coordinate frames have already been defined. Derive the Jacobian matrix for this robot which relates joint velocities to end-effector velocities. Specifically, you should compute: [[(v_(0,t)^(0))],[(\omega _(0,3)^(0))]]=J[[q_(1)^(?)],[q_(2)^(?)],[q_(3)^(?)]] where v_(0,t)^(0) is the linear velocity of the point t of the end-effector with respect to the base frame {0} represented in base frame {0},\omega _(0,3)^(0) is the angular velocity of frame {3} with respect to the base frame {0} represented in base frame {0}, and q_(1)^(?),q_(2)^(?),q_(3)^(?), are the joint velocities. HINT: To make the process of computing the Jacobian matrix easier, you are free to use Theorem 3.3 in the book. Figure 1: PUMA robot for Problem 1.