(Solved): Problem 1: Graphing a Function (18 points) Sketch the graph of a function \( f \) satisfying all of ...

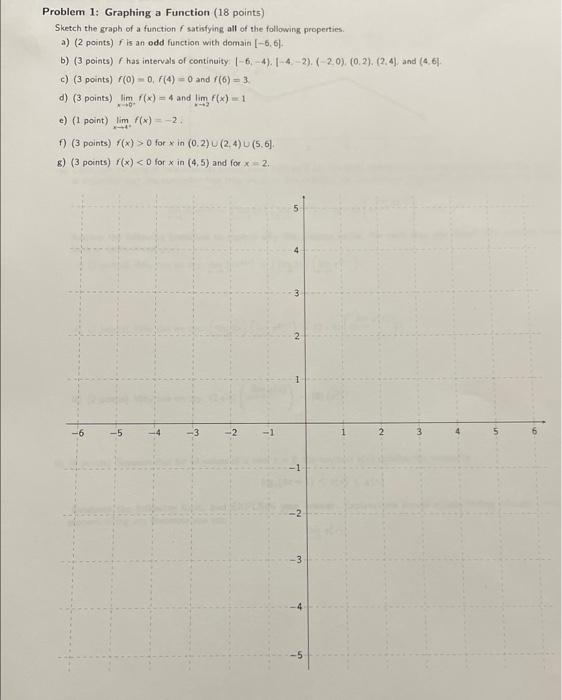
Problem 1: Graphing a Function (18 points) Sketch the graph of a function \( f \) satisfying all of the following properties. a) (2 points) fis an odd function with domain \( [-6,6] \). b) \( (3 \) points \( ) \) f has intervals of continuity: \( (-6,-4) .,-4,-2),(-2,0),(0,2),(2,4\} \), and \( (4,6\} \). c) \( (3 \) points \( ) f(0)=0, f(4)=0 \) and \( f(6)=3 . \) d) (3 points) \( \lim _{x \rightarrow 0^{+}} f(x)=4 \) and \( \lim _{x \rightarrow 2} f(x)=1 \) e) (1 point) \( \lim _{x \rightarrow 4^{+}} f(x)=-2 \). f) \( (3 \) points \( ) f(x)>0 \) for \( x \) in \( (0,2) \cup(2,4) \cup(5,6) \), g) \( (3 \) points) \( f(x)<0 \) for \( x \) in \( (4,5) \) and for \( x=2 \).