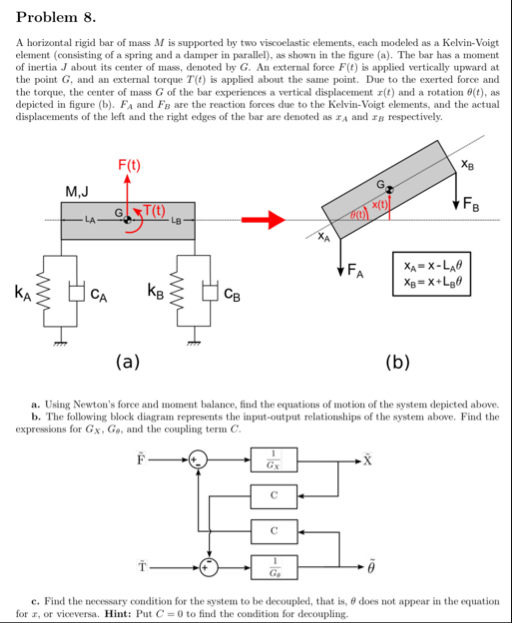
(Solved): Problem 8. A horizontal rigid bar of mass M is supported by two viscoelastic elements, each modeled ...
Problem 8. A horizontal rigid bar of mass
Mis supported by two viscoelastic elements, each modeled as a Kelvin-Voigt element (consisting of a spring and a damper in parallel), as shown in the figure (a). The bar has a moment of inertia
Jabout its center of mass, denoted by
G. An external force
F(t)is applied vertically upward at the point
G, and an external torque
T(t)is applied about the same point. Due to the exerted force and the torque, the center of mass
Gof the bar experiences a vertical displacement
x(t)and a rotation
\theta (t), as depicted in figure (b).
F_(A)and
F_(B)are the reaction forces due to the Kelvin-Voigt elements, and the actual displacements of the left and the right edges of the bar are denoted as
x_(A)and
x_(B)respectively. a. Using Newton's force and moment balance, find the equations of motion of the system depicted above. b. The following block diagram represents the input-output relationships of the system above. Find the expressions for
G_(x),G_(\theta ), and the coupling term
C. c. Find the necessary condition for the system to be decoupled, that is,
\theta does not appear in the equation for
x, or viceversa. Hint: Put
C=0to find the condition for decoupling.