(Solved): Q6. Figure Q6 shows a simply supported beam with constant value of \( E I \) throughout the beam spa ...

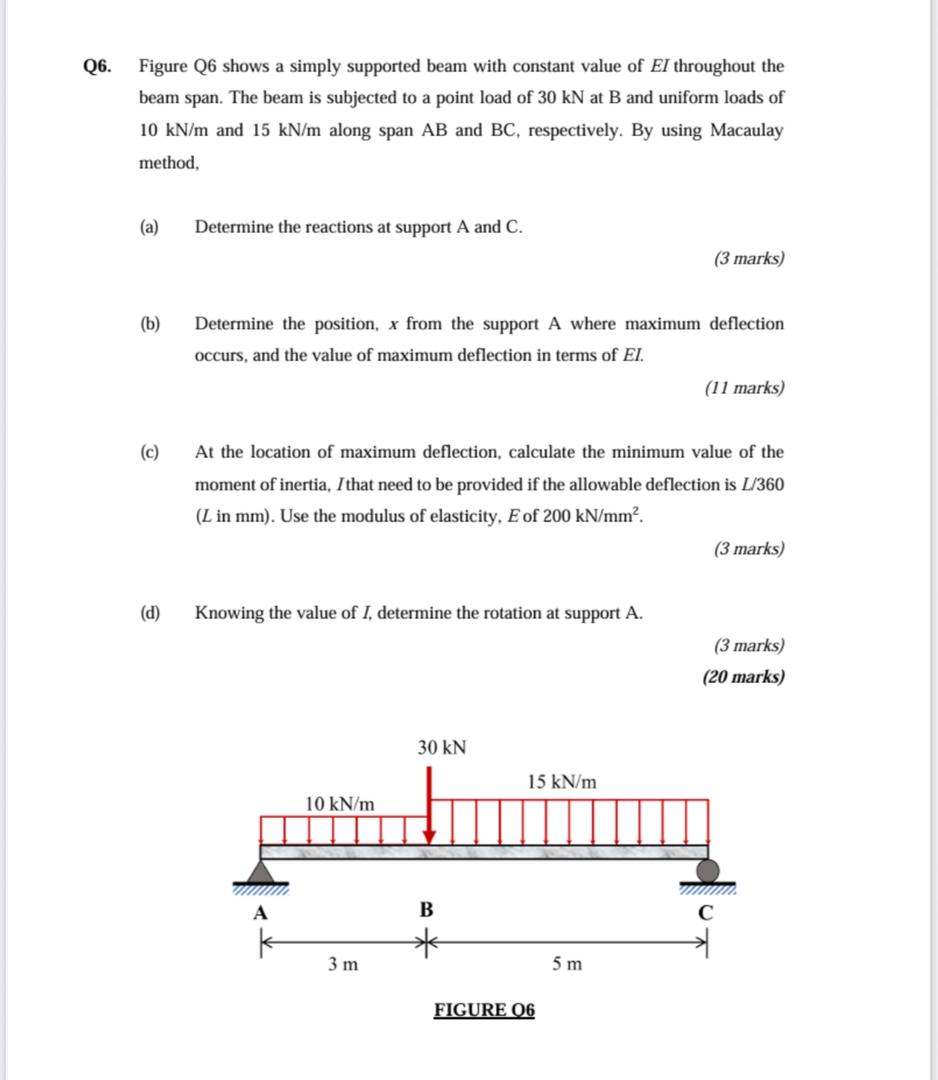
Q6. Figure Q6 shows a simply supported beam with constant value of \( E I \) throughout the beam span. The beam is subjected to a point load of 30 kN at B and uniform loads of \( 10 \mathrm{kN} / \mathrm{m} \) and \( 15 \mathrm{kN} / \mathrm{m} \) along span AB and BC, respectively. By using Macaulay method, (a) Determine the reactions at support A and C. (b) Determine the position, \( x \) from the support A where maximum deflection occurs, and the value of maximum deflection in terms of \( E I \). (11 marks) (c) At the location of maximum deflection, calculate the minimum value of the moment of inertia, \( I \) that need to be provided if the allowable deflection is \( L / 360 \) ( \( L \) in mm ). Use the modulus of elasticity, \( E \) of \( 200 \mathrm{kN} / \mathrm{mm}^{2} \). (d) Knowing the value of \( I \), determine the rotation at support A.