Home /
Expert Answers /
Advanced Math /
question-1-l-u-1-t-t-8-e-s-1-s-2-k-s-where-k-question-2-if-m-gamma-k-0-then-a-pa552
(Solved): Question 1 L{u_(1)(t)[t 8]}=e^(-s)((1)/(s^(2)) (k)/(s)) where k= Question 2 If m,\gamma ,k!=0 then a ...
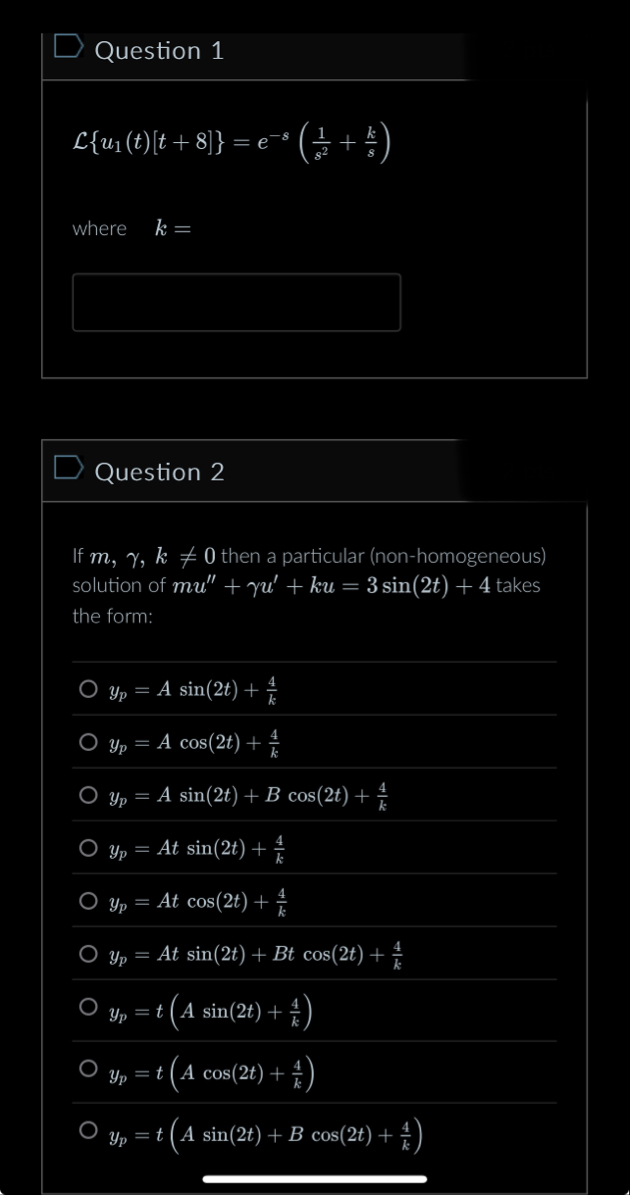
Question 1
L{u_(1)(t)[t 8]}=e^(-s)((1)/(s^(2)) (k)/(s))where
k=Question 2 If
m,\gamma ,k!=0then a particular (non-homogeneous) solution of
\mu ^('') \gamma u^(') ku=3sin(2t) 4takes the form:
y_(p)=Asin(2t) (4)/(k)
y_(p)=Acos(2t) (4)/(k)
y_(p)=Asin(2t) Bcos(2t) (4)/(k)
y_(p)=Atsin(2t) (4)/(k)
y_(p)=Atcos(2t) (4)/(k)
y_(p)=Atsin(2t) Btcos(2t) (4)/(k)
y_(p)=t(Asin(2t) (4)/(k))
y_(p)=t(Acos(2t) (4)/(k))
y_(p)=t(Asin(2t) Bcos(2t) (4)/(k))