(Solved): Question 5 0/2 pts 2 99 Details Quick note: Please use the one-sample t test and one-sample t confid ...

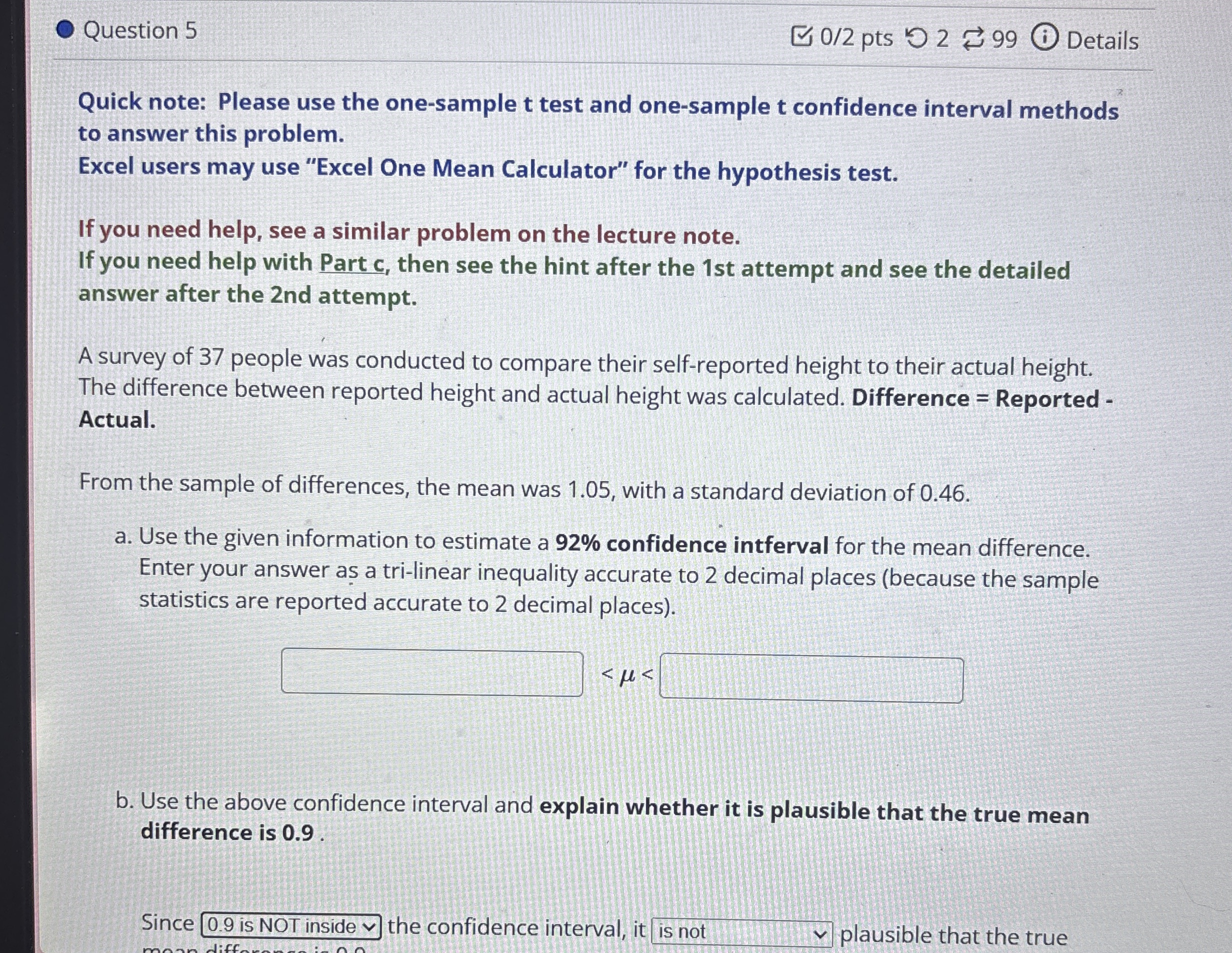
Question 5 0/2 pts 2 99 Details Quick note: Please use the one-sample

test and one-sample t confidence interval methods to answer this problem. Excel users may use "Excel One Mean Calculator" for the hypothesis test. If you need help, see a similar problem on the lecture note. If you need help with Part c, then see the hint after the 1st attempt and see the detailed answer after the 2nd attempt. A survey of 37 people was conducted to compare their self-reported height to their actual height. The difference between reported height and actual height was calculated. Difference

Reported Actual. From the sample of differences, the mean was 1.05 , with a standard deviation of 0.46. a. Use the given information to estimate a

confidence intferval for the mean difference. Enter your answer as a tri-linear inequality accurate to 2 decimal places (because the sample statistics are reported accurate to 2 decimal places).

b. Use the above confidence interval and explain whether it is plausible that the true mean difference is 0.9 . Since

0.9 is NOT inside

the confidence interval, it

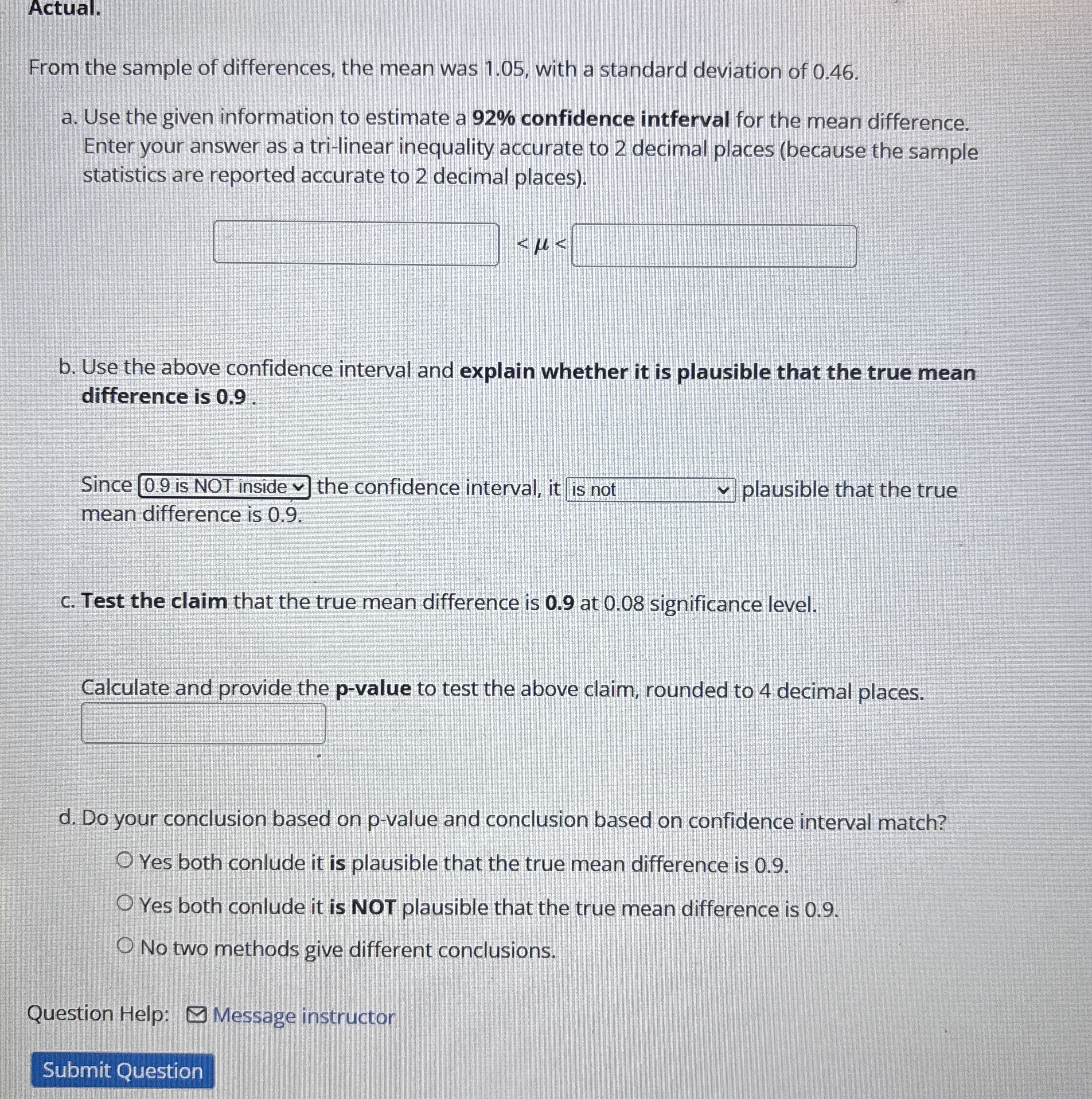
is not plausible that the trueActual. From the sample of differences, the mean was 1.05, with a standard deviation of 0.46 . a. Use the given information to estimate a

confidence intferval for the mean difference. Enter your answer as a tri-linear inequality accurate to 2 decimal places (because the sample statistics are reported accurate to 2 decimal places).

b. Use the above confidence interval and explain whether it is plausible that the true mean difference is 0.9 . Since 0.9 is NOT inside

the confidence interval, it is

] plausible that the true mean difference is 0.9 . c. Test the claim that the true mean difference is

at 0.08 significance level. Calculate and provide the p-value to test the above claim, rounded to 4 decimal places.

d. Do your conclusion based on p-value and conclusion based on confidence interval match? Yes both conlude it is plausible that the true mean difference is 0.9 . Yes both conlude it is NOT plausible that the true mean difference is 0.9. No two methods give different conclusions. Question Help: Message instructor