Home /
Expert Answers /
Electrical Engineering /
question2-a-continuous-time-system-has-the-following-functionalities-it-gene-pa250
(Solved): Question2 A continuous-time system has the following functionalities: it gene ...
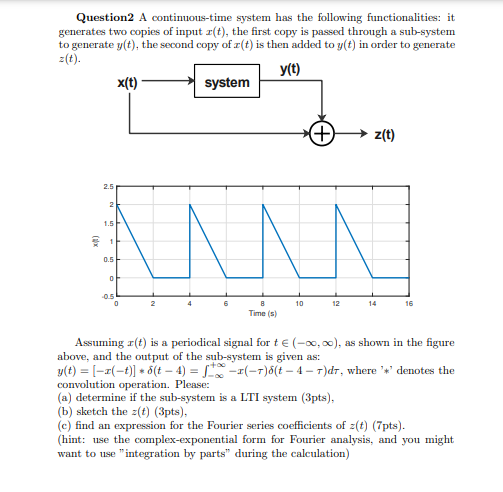
Question2 A continuous-time system has the following functionalities: it generates two copies of input , the first copy is passed through a sub-system to generate , the second copy of is then added to in order to generate Assuming is a periodical signal for , as shown in the figure above, and the output of the sub-system is given as: , where '*' denotes the convolution operation. Please: (a) determine if the sub-system is a LTI system (3pts), (b) sketch the , (c) find an expression for the Fourier series coefficients of (7pts). (hint: use the complex-exponential form for Fourier analysis, and you might want to use "integration by parts" during the calculation)
Expert Answer
a)Please refer to the below solution if the sub-system is a LTI system.To determine if a system is linear, we need to answer the following question: When an input signal is applied to the system, does the output response exhibit homogeneity and additivity? If a system is both homogeneous and additive, it is a linear system.One test to verify time invariance/variance property of a system is to shift the response of the system to an input signal and apply a shifted input, to the same system and compare the two waveforms, so obtained. If the system is time invariant, the two waveforms will match when the input and output shifts match.