Home /
Expert Answers /
Computer Science /
questions-question-1-turing-machine-computation-consider-a-turing-machine-m-with-states-q-q-0-q-pa848
(Solved): Questions Question 1-Turing Machine computation Consider a Turing Machine M with states Q={q_(0),q_( ...
Questions
Question 1-Turing Machine computation
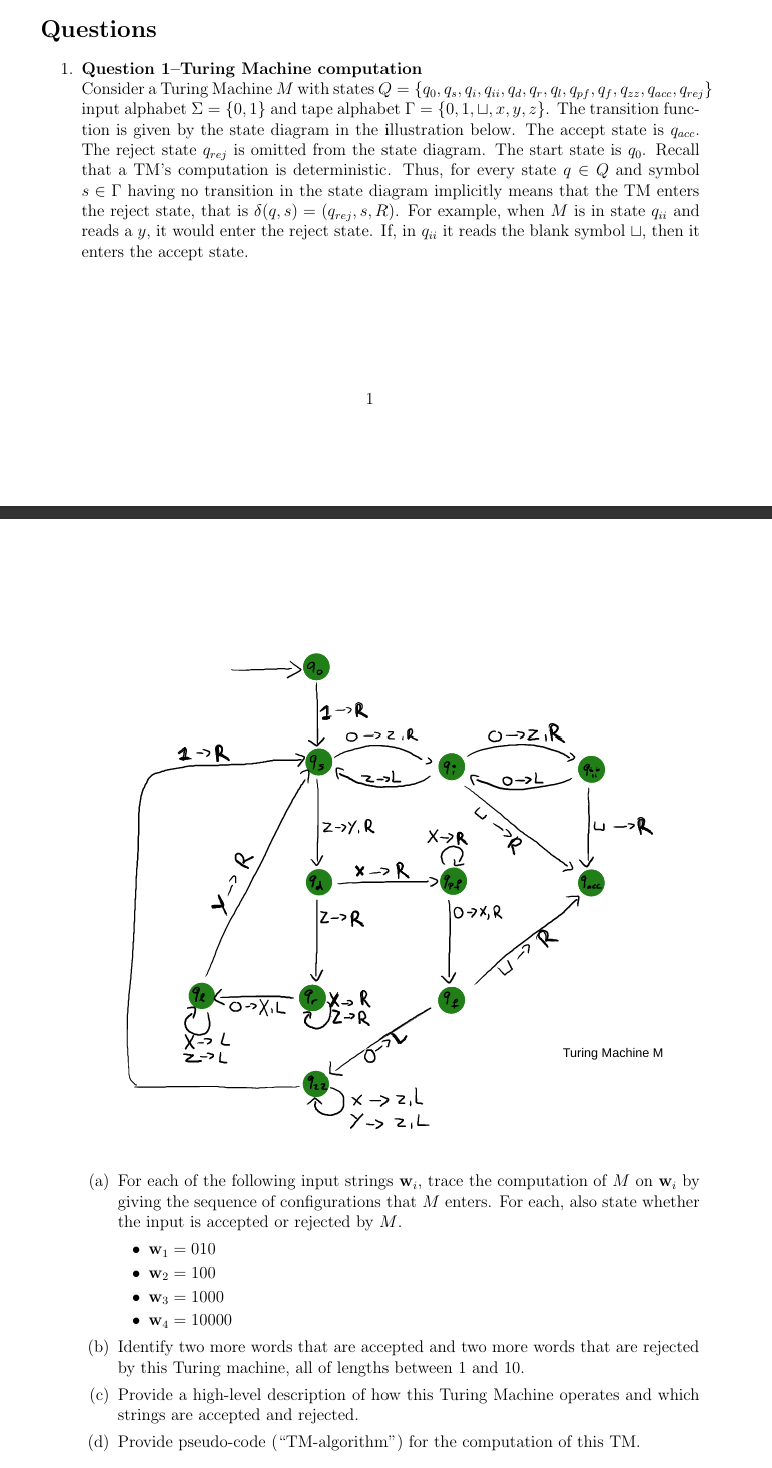
Consider a Turing Machine M with states Q={q_(0),q_(s),q_(i),q_(ii),q_(d),q_(r),q_(l),q_(pf),q_(f),q_(zz),q_(acc),q_(rej)} input alphabet \Sigma ={0,1} and tape alphabet \Gamma ={0,1,?,x,y,z}. The transition function is given by the state diagram in the illustration below. The accept state is q_(acc). The reject state q_(rej) is omitted from the state diagram. The start state is q_(0). Recall that a TM's computation is deterministic. Thus, for every state qinQ and symbol sin\Gamma having no transition in the state diagram implicitly means that the TM enters the reject state, that is \delta (q,s)=(q_(rej),s,R). For example, when M is in state q_(ii) and reads a y, it would enter the reject state. If, in q_(ii) it reads the blank symbol ?, then it enters the accept state.
1
(a) For each of the following input strings w_(i), trace the computation of M on w_(i) by giving the sequence of configurations that M enters. For each, also state whether the input is accepted or rejected by M.
w_(1)=010
w_(2)=100
w_(3)=1000
w_(4)=10000
(b) Identify two more words that are accepted and two more words that are rejected by this Turing machine, all of lengths between 1 and 10.
(c) Provide a high-level description of how this Turing Machine operates and which strings are accepted and rejected.
(d) Provide pseudo-code ("TM-algorithm") for the computation of this TM.