Home /
Expert Answers /
Other Math /
real-analysis-topology-3-let-f-mathbb-r-k-rightarrow-mathbb-r-and-g-mathbb-r-pa807
(Solved): real analysis topology 3. Let \( f: \mathbb{R}^{k} \rightarrow \mathbb{R} \) and \( g: \mathbb{R} ...
real analysis? topology
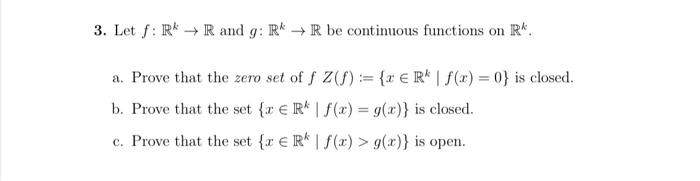
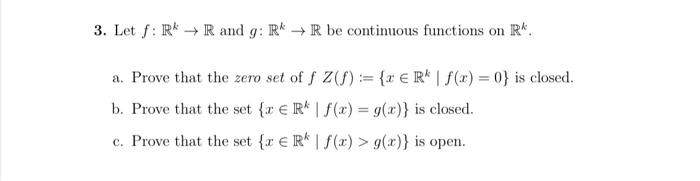
3. Let \( f: \mathbb{R}^{k} \rightarrow \mathbb{R} \) and \( g: \mathbb{R}^{k} \rightarrow \mathbb{R} \) be continuous functions on \( \mathbb{R}^{k} \). a. Prove that the zero set of \( f Z(f):=\left\{x \in \mathbb{R}^{k} \mid f(x)=0\right\} \) is closed. b. Prove that the set \( \left\{x \in \mathbb{R}^{k} \mid f(x)=g(x)\right\} \) is closed. c. Prove that the set \( \left\{x \in \mathbb{R}^{k} \mid f(x)>g(x)\right\} \) is open.
Expert Answer
Given that f:Rk?Randg:Rk?R be continuous function (a) to prove that Z(f)={x?Rk?f(x)=0} is closed Since we know that A function f(x) will be continuous