(Solved): Refer to the unit circle and the ranges of the inverse trigonometric functions. The angle \( \frac{ ...

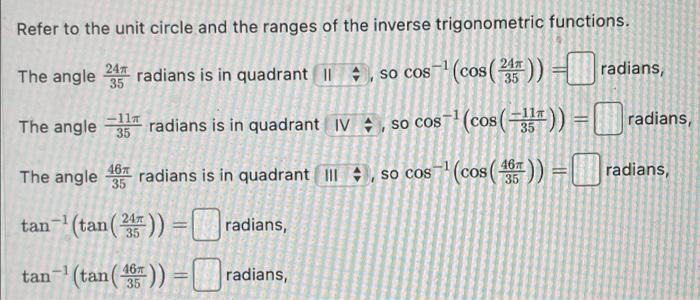
Refer to the unit circle and the ranges of the inverse trigonometric functions. The angle \( \frac{24 \pi}{35} \) radians is in quadrant _, so \( \cos ^{-1}\left(\cos \left(\frac{24 \pi}{35}\right)\right)= \) radians, The angle \( \frac{-11 \pi}{35} \) radians is in quadrant \( \quad \), so \( \cos ^{-1}\left(\cos \left(\frac{-11 \pi}{35}\right)\right)= \) radians, The angle \( \frac{46 \pi}{35} \) radians is in quadrant \( \quad \), so \( \cos ^{-1}\left(\cos \left(\frac{46 \pi}{35}\right)\right)= \) radians, \( \begin{array}{ll}\tan ^{-1}\left(\tan \left(\frac{24 \pi}{35}\right)\right)= & \text { radians, } \\ \tan ^{-1}\left(\tan \left(\frac{46 \pi}{35}\right)\right)=\quad \text { radians, }\end{array} \)