(Solved): Review Learning Goal: As shown, I-beam ABC supports a sign that weighs S=21lb. The I -beam is 30 in ...
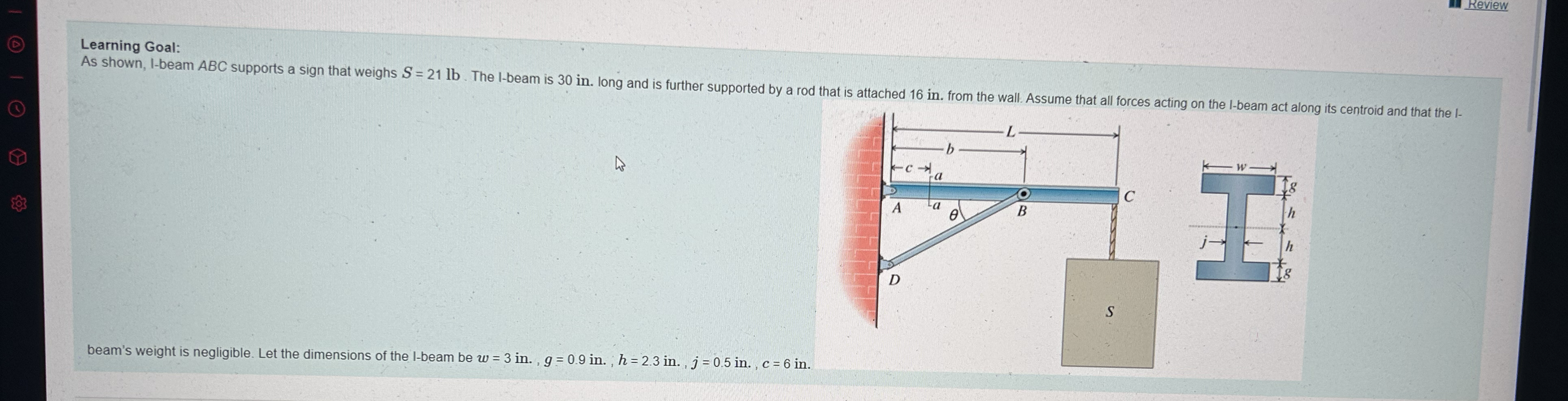
Review Learning Goal: As shown, I-beam ABC supports a sign that weighs
S=21lb. The I -beam is 30 in . long and is further supported by a rod that is attached 16 in. from the wall. Assume that all forces acting on the
I-beam act along its centroid and that the
I- beam's weight is negligible. Let the dimensions of the I-beam be
w=3in.
g=0.9in.
h=2.3in.
j=0.5in. ,
c=6in.
ABCxABC
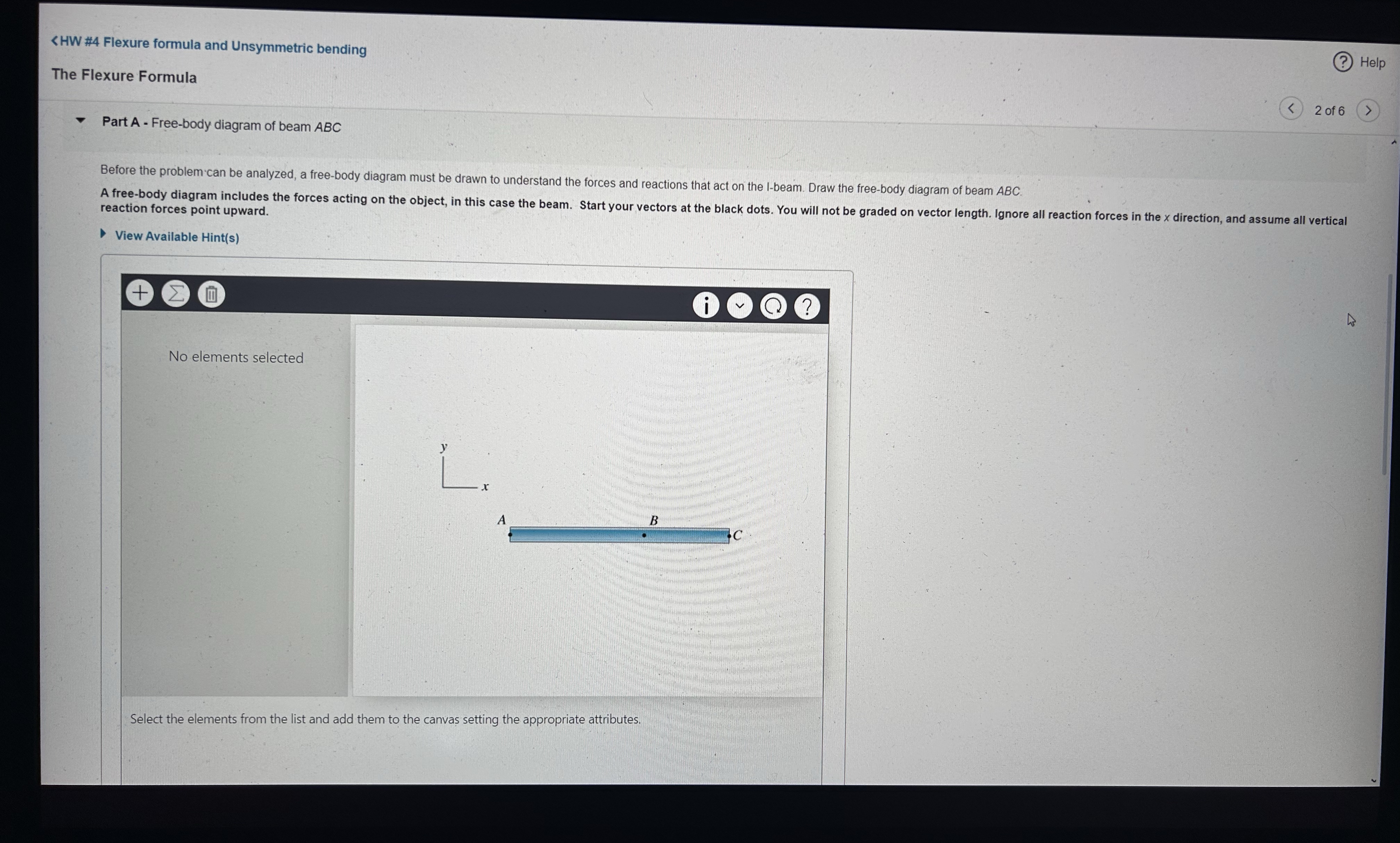
Before the problem can be analyzed, a free-body diagram must be drawn to understand the forces and reactions that act on the l-beam. Draw the free-body diagram of beam ABC.
A free-body diagram includes the forces acting on the object, in this case the beam. Start your vectors at the black dots. You will not be graded on vector length. Ignore all reaction forces in the x direction, and assume all vertical reaction forces point upward.
View Available Hint(s)
No elements selected
Select the elements from the list and addThe Flexure Formula Part B - Moment of inertia of beam ABC Determine the moment of inertia
Iof I-beam ABC. Recall that in an I-beam, the flanges are the horizontal top and bottom sections and the web is the vertical section between the two flanges. Express your answer to three significant figures and include the appropriate units. View Available Hint(s)
?
?Part C - Bending moment at section a-a in beam
ABCDetermine the absolute value of the bending moment in the beam at section
a-a which is 6 in. from the wall. Express your answer to three significant figures and include the appropriate units. View Available Hint(s)
|M|=
?
?Part D - Absolute maximum bending stress in section a-a on beam ABC Determine the absolute maximum bending stress in the cross section at cut
a-a using the flexure formula. Express your answer in psi to three significant figures. View Available Hint(s)
|\sigma _(max)|=psi