Home /
Expert Answers /
Advanced Math /
run-matlab-and-show-matlab-file7c-onlyalgorithm-3-5-7-construct-the-clamped-cubic-spline-using-the-pa372
(Solved): run matlab and show matlab file7c. onlyalgorithm 3.5 7. Construct the clamped cubic spline using the ...
run matlab and show matlab file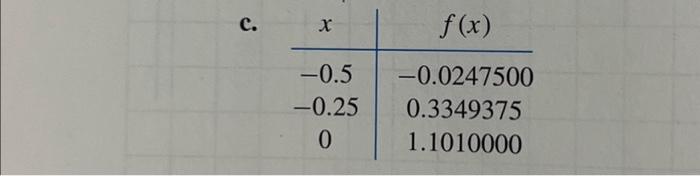

7c. only
algorithm 3.5


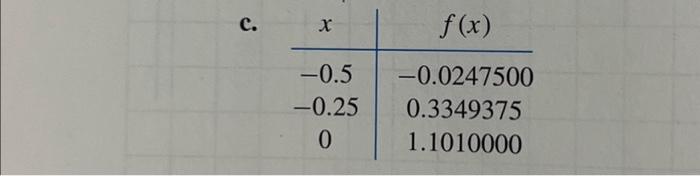

7. Construct the clamped cubic spline using the data of Exercise 3 and the fact that a. and . b. and . c. and . d. and .
c.
To construct the cubic spline interpolant for the function defined at the numbers , satisfying and : INPUT . OUTPUT for . (Note: for .) Step 1 For set . Step 2 Set ; Step 3 For Step 4 Set (Steps 4, 5, and 6 and part of Step 7 solve a tridiagonal linear system using a method described in Algorithm 6.7.) Step 5 For