(Solved): Suppose that 7 Joules of work is needed to stretch a spring from its natural length of \( 14 \mathr ...

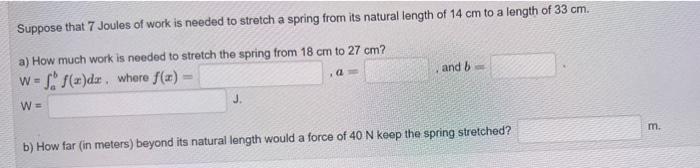
Suppose that 7 Joules of work is needed to stretch a spring from its natural length of \( 14 \mathrm{~cm} \) to a length of \( 33 \mathrm{~cm} \). a) How much work is needed to stretch the spring from \( 18 \mathrm{~cm} \) to \( 27 \mathrm{~cm} \) ? \( W=\int_{a}^{b} f(x) d x \), where \( f(x)= \) and \( b= \) \( \mathrm{W}= \) b) How far (in meters) beyond its natural length would a force of \( 40 \mathrm{~N} \) keep the spring stretched? 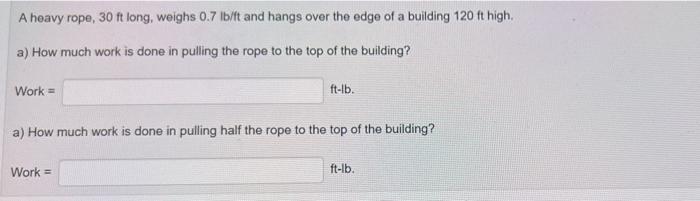A heavy rope, \( 30 \mathrm{ft} \) long, weighs \( 0.7 \mathrm{lb} / \mathrm{ft} \) and hangs over the edge of a building \( 120 \mathrm{ft} \) high. a) How much work is done in pulling the rope to the top of the building? Work = ft-lb. a) How much work is done in pulling half the rope to the top of the building?