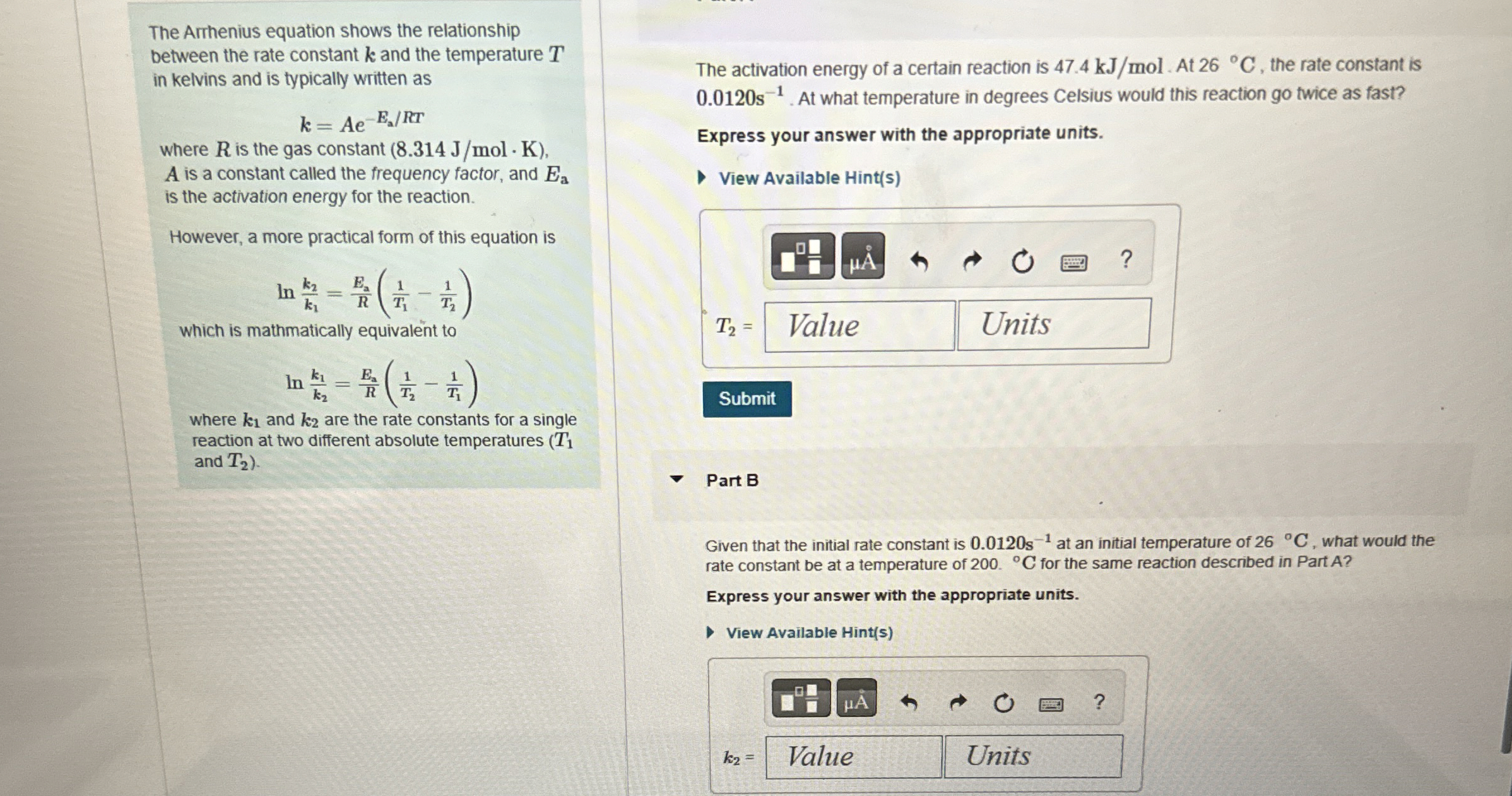
(Solved): The Arrhenius equation shows the relationship between the rate constant k and the temperature T in k ...
The Arrhenius equation shows the relationship between the rate constant
kand the temperature
Tin kelvins and is typically written as
k=Ae^(-(E_(a))/(R)T)where
Ris the gas constant
(8.314(J)/(m)ol*K),
Ais a constant called the frequency factor, and
E_(a)is the activation energy for the reaction. However, a more practical form of this equation is
ln((k_(2))/(k_(1)))=(E_(2))/(R)((1)/(T_(1))-(1)/(T_(2)))which is mathmatically equivalent to
ln((k_(1))/(k_(2)))=(E_(a))/(R)((1)/(T_(2))-(1)/(T_(1)))where
k_(1)and
k_(2)are the rate constants for a single reaction at two different absolute temperatures (
T_(1)and
T_(2)). The activation energy of a certain reaction is
47.4k(J)/(m)ol. At
26\deg C, the rate constant is
0.0120s^(-1). At what temperature in degrees Celsius would this reaction go twice as fast? Express your answer with the appropriate units. View Available Hint(s)
?
q,Part B Given that the initial rate constant is
0.0120s^(-1)at an initial temperature of
26\deg C, what would the rate constant be at a temperature of 200 .
\deg Cfor the same reaction described in Part A? Express your answer with the appropriate units. View Available Hint(s)
k_(2)=
?