Home /
Expert Answers /
Calculus /
the-bounds-of-our-interval-will-be-lt-x-lt-thus-the-volume-of-the-solid-obtained-when-the-region-pa836
(Solved): The bounds of our interval will be <=x<= Thus the volume of the solid obtained when the region ...
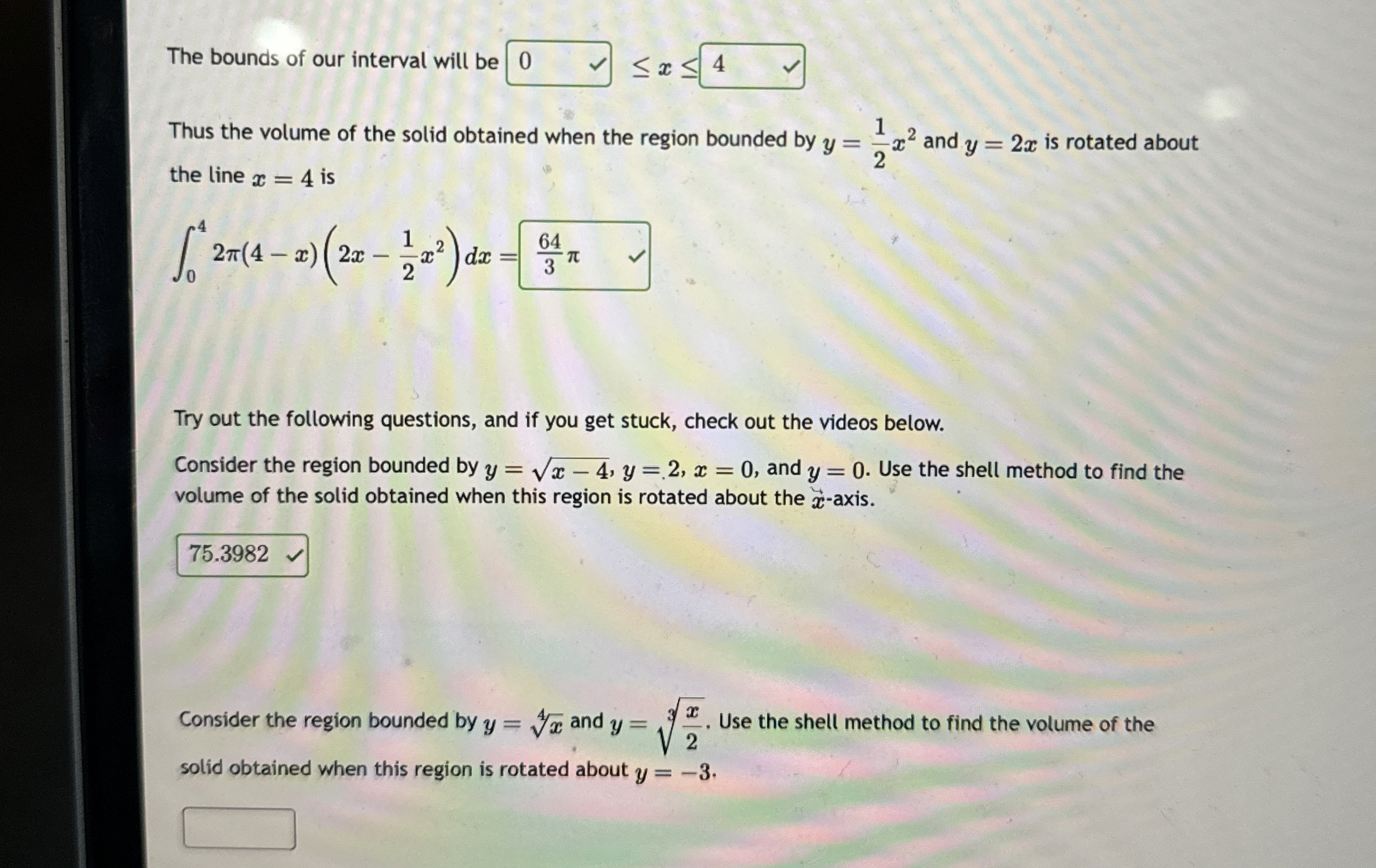
The bounds of our interval will be
<=x<=Thus the volume of the solid obtained when the region bounded by
y=(1)/(2)x^(2)and
y=2xis rotated about the line
x=4is
\int_0^4 2\pi (4-x)(2x-(1)/(2)x^(2))dx=Try out the following questions, and if you get stuck, check out the videos below. Consider the region bounded by
y=\sqrt(x-4),y=2,x=0, and
y=0. Use the shell method to find the volume of the solid obtained when this region is rotated about the
x_(x)-axis. Consider the region bounded by
y=\root(4)(x)and
y=\root(3)((x)/(2)). Use the shell method to find the volume of the solid obtained when this region is rotated about
y=-3.