Home /
Expert Answers /
Geometry /
the-diagram-shows-measurements-for-the-three-triangles-complete-the-table-using-w-as-the-re-pa366
(Solved): The diagram shows measurements for the three triangles. Complete the table using ()/(_(W)) as the re ...
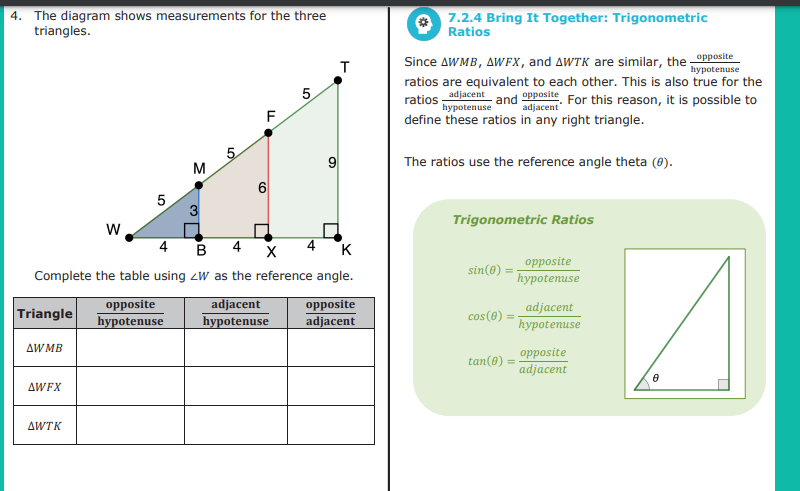
The diagram shows measurements for the three
triangles.
Complete the table using ()/(_(W)) as the reference angle.
7.2.4 Bring It Together: Trigonometric
Ratios
Since ()/(_(()/())WMB)(,)/(_(()/()))WFx, and ()/(_(()/())WTK) are similar, the ( opposite )/( hypotenuse )
ratios are equivalent to each other. This is also true for the
ratios ( adjacent )/( hypotenuse ) and ( opposite )/( adjacent ). For this reason, it is possible to
define these ratios in any right triangle.
The ratios use the reference angle theta (\theta ).
Trigonometric Ratios
sin(\theta )=( opposite )/( hypotenuse )
cos(\theta )=( adjacent )/( hypotenuse )
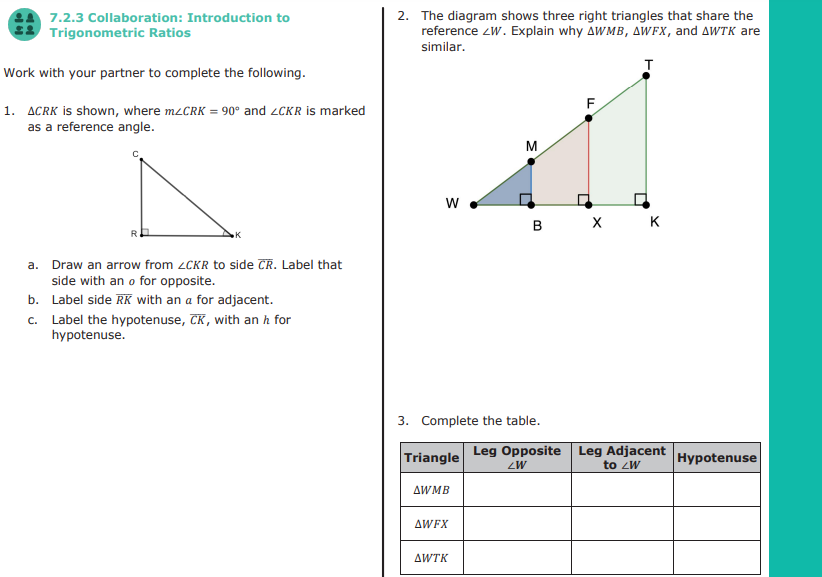
tan(\theta )=( opposite )/( adjacent ) Work with your partner to complete the following.
()/(_(()/())CRK) is shown, where (m)/(_(C))RK=90\deg and ()/(_(C)KR) is marked
as a reference angle.
a. Draw an arrow from ()/(_(C)KR) to side ()/(bar) (CR). Label that
side with an o for opposite.
b. Label side ()/(bar) (RK) with an a for adjacent.
c. Label the hypotenuse, ()/(bar) (CK), with an h for
hypotenuse.
Complete the table. Ask two classmates for the "Notice and Wonder" what
they wrote for both triangles. Record their responses
below. You are the only person who should write in the
first three columns of the table. Have the person initial
that it is written correctly.
Write a conjecture for each of the right triangles that
were drawn.
The triangles drawn by you and your classmates during
the Exploration vary. Using either the triangles explored
in Questions 1-3 or Questions 4-6, explain why these
triangles are similar.
Right triangles with one other congruent angle
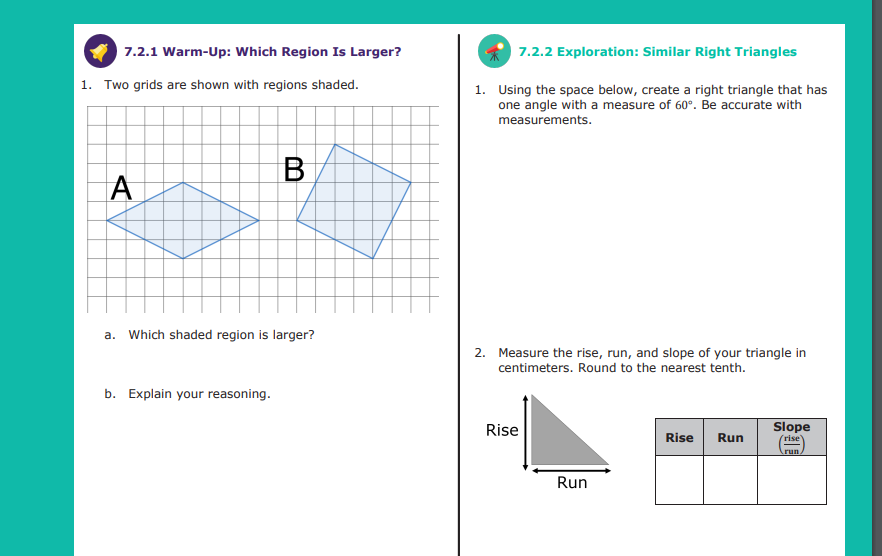
are similar because of AA similarity. 7.2.1 Warm-Up: Which Region Is Larger?
Two qrids are shown with reqions shaded.
a. Which shaded region is larger?
b. Explain your reasoning.
7.2.2 Exploration: Similar Right Triangles
Using the space below, create a right triangle that has
one angle with a measure of 60\deg . Be accurate with
measurements.
Measure the rise, run, and slope of your triangle in
centimeters. Round to the nearest tenth.Ask two classmates for the "Notice and Wonder" what
they wrote for both triangles. Record their responses
below. You are the only person who should write in the
first three columns of the table. Have the person initial
that it is written correctly.
Write a conjecture for each of the right triangles that
were drawn.
The triangles drawn by you and your classmates during
the Exploration vary. Using either the triangles explored
in Questions 1-3 or Questions 4-6, explain why these
triangles are similar.
Right triangles with one other congruent angle
are similar because of AA similarity.