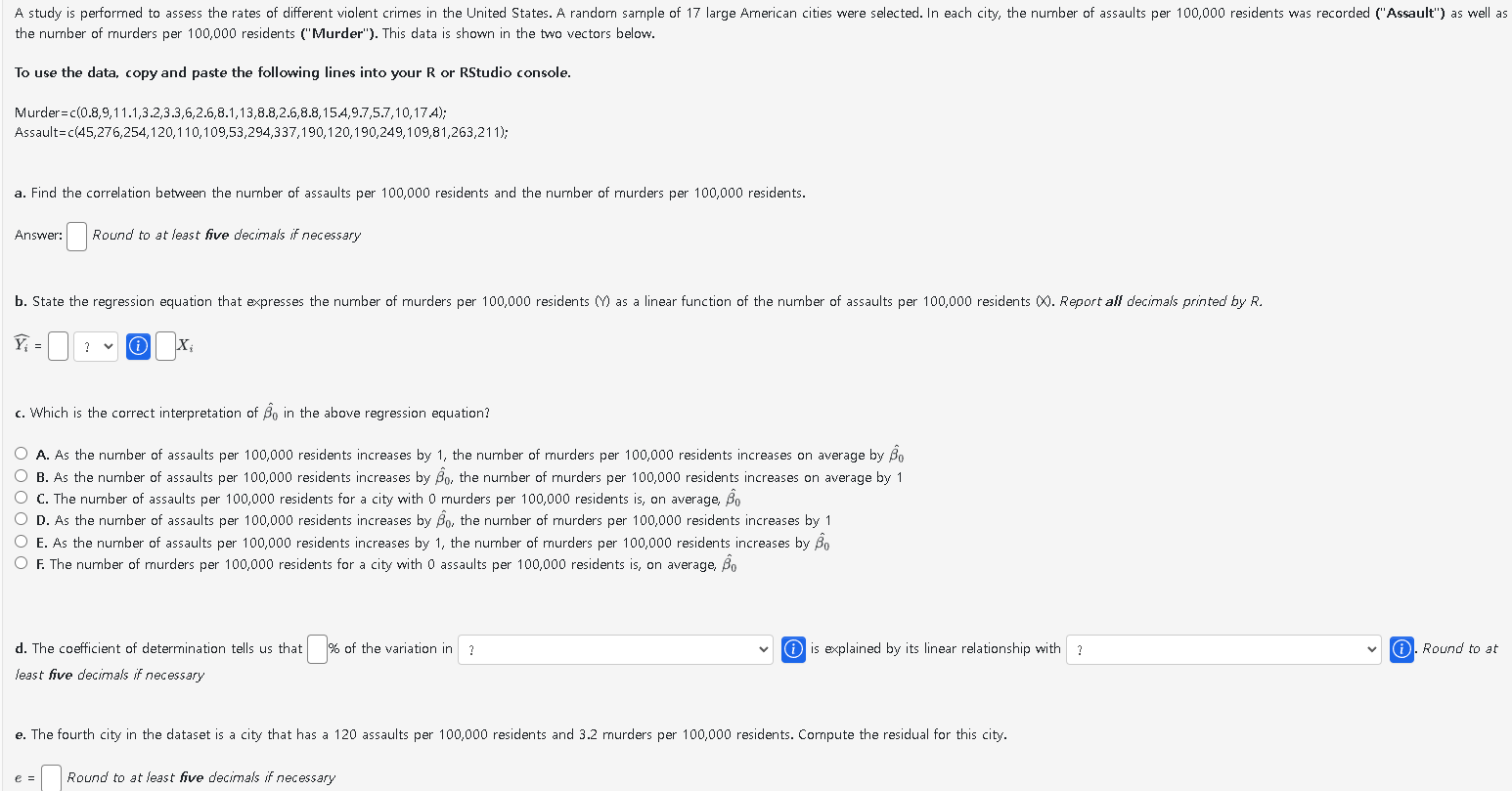
(Solved): the number of murders per 100,000 residents ("Murder"). This data is shown in the two vectors below. ...

the number of murders per 100,000 residents ("Murder"). This data is shown in the two vectors below. To use the data, copy and paste the following lines into your R or RStudio console. Murder =c(0.8,9,11.1,3.2,3.3,6,2.6,8.1,13,8.8,2.6,8.8,15.4,9.7,5.7,10,17.4); Assault =c(45,276,254,120,110,109,53,294,337,190,120,190,249,109,81,263,211); a. Find the correlation between the number of assaults per 100,000 residents and the number of murders per 100,000 residents. Answer: Round to at least five decimals if necessary b. State the regression equation that expresses the number of murders per 100,000 residents as a linear function of the number of assaults per 100,000 residents 0 . Report all decimals printed by R. widehat(Y_(i))=vv (i) ?x_(i) c. Which is the correct interpretation of hat(\beta )_(0) in the above regression equation? A. As the number of assaults per 100,000 residents increases by 1 , the number of murders per 100,000 residents increases on average by hat(\beta _(0)) B. As the number of assaults per 100,000 residents increases by hat(\beta )_(0), the number of murders per 100,000 residents increases on average by 1 C. The number of assaults per 100,000 residents for a city with 0 murders per 100,000 residents is, on average, hat(\beta )_(0) D. As the number of assaults per 100,000 residents increases by hat(\beta )_(0), the number of murders per 100,000 residents increases by 1 E. As the number of assaults per 100,000 residents increases by 1 , the number of murders per 100,000 residents increases by hat(\beta )_(0) F. The number of murders per 100,000 residents for a city with 0 assaults per 100,000 residents is, on average, hat(\beta _(0)) d. The coefficient of determination tells us that % of the variation in is explained by its linear relationship with (i). Round to at least five decimals if necessary e. The fourth city in the dataset is a city that has a 120 assaults per 100,000 residents and 3.2 murders per 100,000 residents. Compute the residual for this city. e=, Round to at least five decimals if necessary