(Solved): Use Macaulay's method to determine the deflection of the beam below. The beam is made of steel wit ...

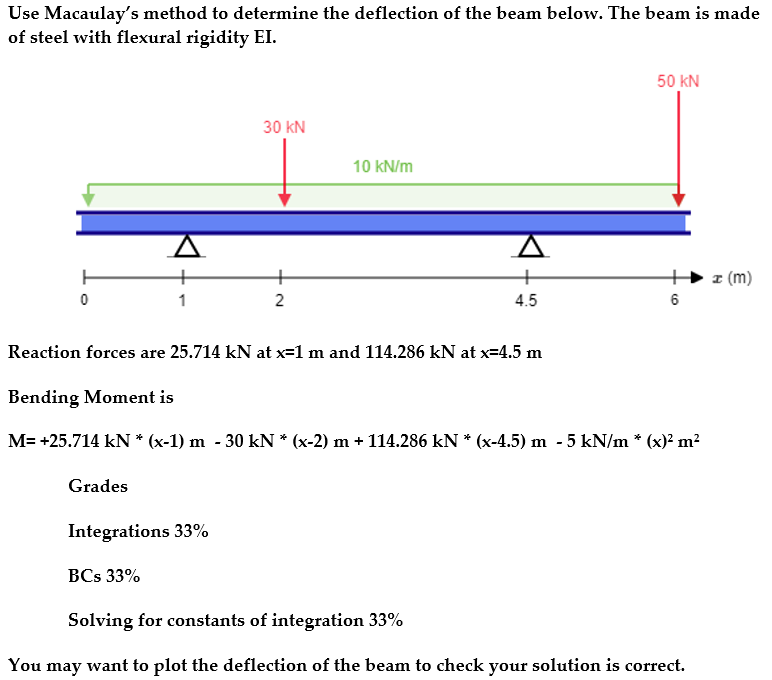
Use Macaulay's method to determine the deflection of the beam below. The beam is made of steel with flexural rigidity EI. Reaction forces are \( 25.714 \mathrm{kN} \) at \( \mathrm{x}=1 \mathrm{~m} \) and \( 114.286 \mathrm{kN} \) at \( \mathrm{x}=4.5 \mathrm{~m} \) Bending Moment is \[ \mathrm{M}=+25.714 \mathrm{kN} *(\mathrm{x}-1) \mathrm{m}-30 \mathrm{kN} *(\mathrm{x}-2) \mathrm{m}+114.286 \mathrm{kN}{ }^{*}(\mathrm{x}-4.5) \mathrm{m}-5 \mathrm{kN} / \mathrm{m}^{*}\left(\mathrm{x}^{2} \mathrm{~m}^{2}\right. \] Grades Integrations \( 33 \% \) BCs \( 33 \% \) Solving for constants of integration \( 33 \% \) You may want to plot the deflection of the beam to check your solution is correct.