(Solved): Use the contingency table to the right to complete parts (a) through (c) below a. Find the expected ...

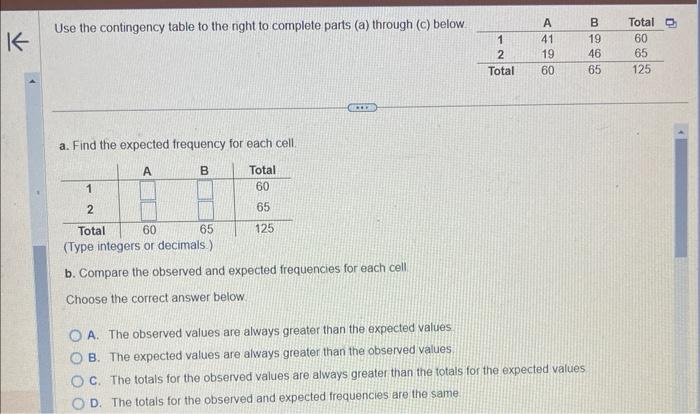
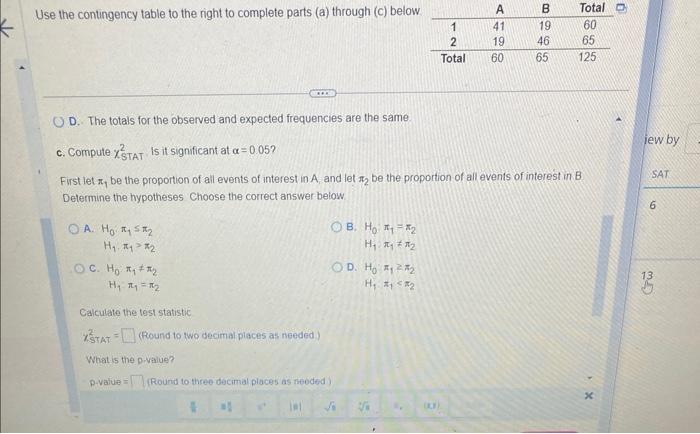
Use the contingency table to the right to complete parts (a) through (c) below a. Find the expected frequency for each cell. (lypentegers or decimais.) b. Compare the observed and expected frequencies for each cell Choose the correct answer below A. The observed values are always greater than the expected values Use the contingency table to the right to complete parts (a) through (c) below. D. The totals for the observed and expected frequencies are the same. c. Compute \( \gamma_{\text {STAT }}^{2} \) is it significant at \( \alpha=0.05 \) ? First let \( \pi_{1} \) be the proportion of all events of interest in \( \mathrm{A} \), and let \( \pi_{2} \) be the proportion of all events of interest in B Determine the hypotheses Choose the correct answer beiow A. \( H_{0}: \pi_{1} \leq \pi_{2} \) B. \( H_{0}: \pi_{1}=\pi_{2} \) \( H_{1}, \pi_{1}>\pi_{2} \) \( H_{1}=\pi_{1} \neq \pi_{2} \) C. \( H_{0} \pi_{1} \neq \pi_{2} \) D. \( \mathrm{H}_{0} \cdot \pi_{1} \geq \pi_{2} \) \( H_{1}-\pi_{1}=\pi_{2} \) \( H_{1}=\pi_{1}<\pi_{2} \) Calculate the test statistic \( x_{\text {STAT }}^{2} \) (Round to two decimal piaces as needed) What is the DNalue? 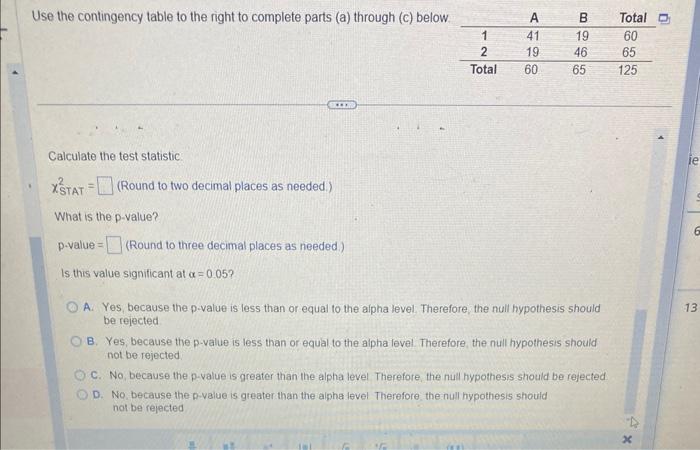p-vaiue = (Round to three decimal places as needed) x) Use the contingency table to the right to complete parts (a) through (c) below. Calculate the test statistic \( x_{\text {STAT }}^{2}= \) (Round to two decimal places as needed.) What is the p-value? p-value = (Round to three decimal places as needed.) Is this value significant at \( \alpha=0.05 \) ? A. Yes, because the p.value is less than or equal to the alpha level. Therefore the null hypothesis should be rejected B. Yes, because the p-value is less than or equal to the alpha level Therefore, the null hypothesis should not be rejected. C. No, because the p-value is greater than the alpha level Therefore, the null hypothesis should be rejected D. No, because the p-value is greater than the alpha fevel Therefore, the nul hypothesis should not be rejected