(Solved): Verify Property 2 of the definition of a probability density function over the given interval. \[ ...

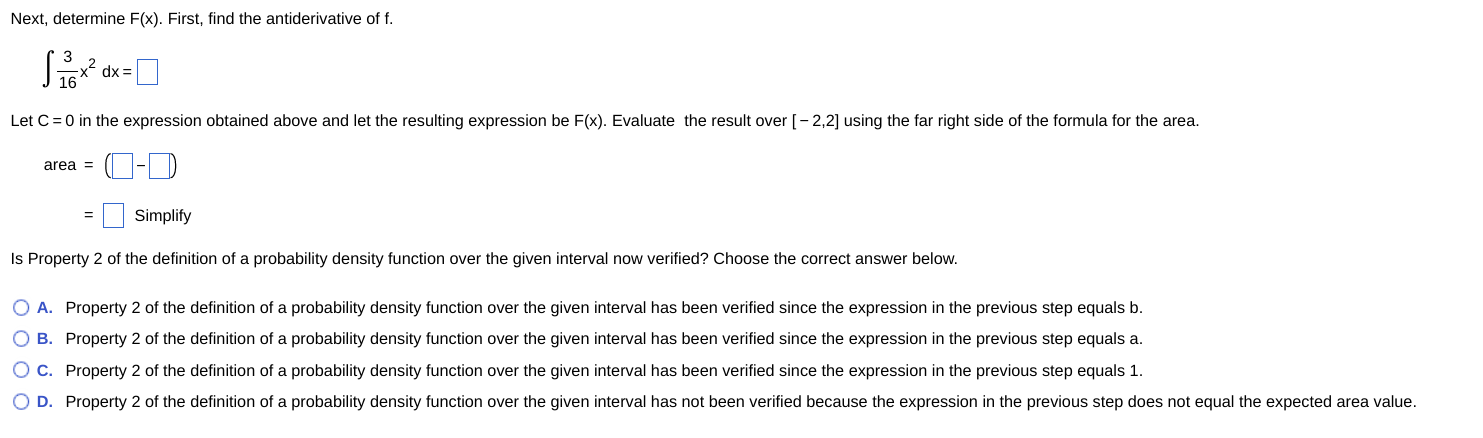
Verify Property 2 of the definition of a probability density function over the given interval. \[ f(x)=\frac{3}{16} x^{2}, \quad[-2,2] \] What is Property 2 of the definition of a probability density function? A. The area under the graph of \( f \) over the interval \( [a, b] \) is \( b \). B. The area under the graph of \( f \) over the interval \( [a, b] \) is 1 . C. The area under the graph of \( f \) over the interval \( [a, b] \) is \( a \). Identify the formula for calculating the area under the graph of the function \( y=f(x) \) over the interval \( [a, b] \). Choose the correct answer below. A. \[ \int_{b}^{a} f(x) d x=[F(x)]_{b}^{a}=F(b)-F(a) \] B. \( \int_{b}^{a} f(x) d x=[F(x)]_{b}^{a}=F(a)-F(b) \) C. \( \int_{a}^{b} f(x) d x=[F(x)]_{a}^{b}=F(a)-F(b) \) D. \( \int_{a}^{b} f(x) d x=[F(x)]_{a}^{b}=F(b)-F(a) \) Substitute \( a, b \), and \( f(x) \) into the left side of the formula from the previous step. \[ \text { area }=\int \frac{3}{16} x^{2} d x \] Next, determine \( \mathrm{F}(\mathrm{x}) \). First, find the antiderivative of \( \mathrm{f} \). \[ \int \frac{3}{16} x^{2} d x= \] Let \( \mathrm{C}=0 \) in the expression obtained above and let the resulting expression be \( \mathrm{F}(\mathrm{x}) \). Evaluate the result over \( [-2,2] \) using the far right side of the formular \[ \begin{aligned} \text { area } & =(\square- \\ & =\text { Simplify } \end{aligned} \] Is Property 2 of the definition of a probability density function over the given interval now verified? Choose the correct answer below.