Home /
Expert Answers /
Advanced Math /
we-consider-the-non-homogeneous-problem-y-39-39-30-18x-x-4-first-we-consider-the-homogeneous-probl-pa915
(Solved): We consider the non-homogeneous problem y^('')=30(18x-x^(4)) First we consider the homogeneous probl ...
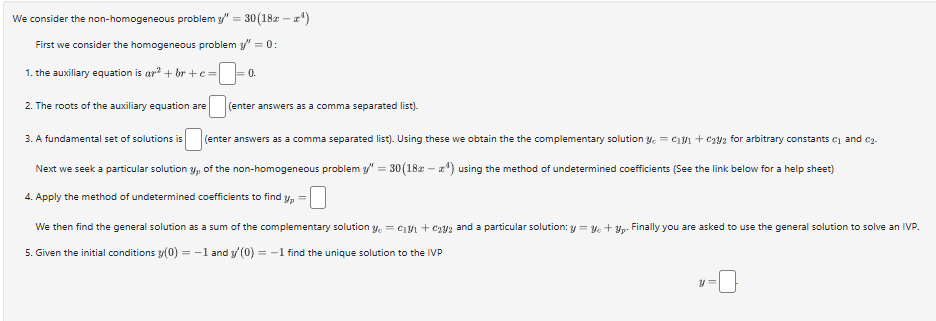
We consider the non-homogeneous problem y^('')=30(18x-x^(4))
First we consider the homogeneous problem y^('')=0 :
the auxiliary equation is ar^(2)+br+c=,=0.
The roots of the auxiliary equation are (enter answers as a comma separated list).
A fundamental set of solutions is (enter answers as a comma separated list). Using these we obtain the the complementary solution y_(c)=c_(1)y_(1)+c_(2)y_(2) for arbitrary constants c_(1) and c_(2).
Next we seek a particular solution y_(p) of the non-homogeneous problem y^('')=30(18x-x^(4)) using the method of undetermined coefficients (See the link below for a help sheet)
Apply the method of undetermined coefficients to find y_(p)=
We then find the general solution as a sum of the complementary solution y_(c)=c_(1)y_(1)+c_(2)y_(2) and a particular solution: y=y_(c)+y_(p). Finally you are asked to use the general solution to solve an IVP.
Given the initial conditions y(0)=-1 and y^(')(0)=-1 find the unique solution to the IVP
y=