Home /
Expert Answers /
Advanced Math /
we-wish-to-solve-the-system-vec-x-39-2-1-0-1-vec-x-sin-t-e-t-via-eigenvector-decom-pa662
(Solved): We wish to solve the system vec(x)^(')=[[2,-1],[0,1]]vec(x)+[[sin(t)],[e^(t)]] via eigenvector decom ...
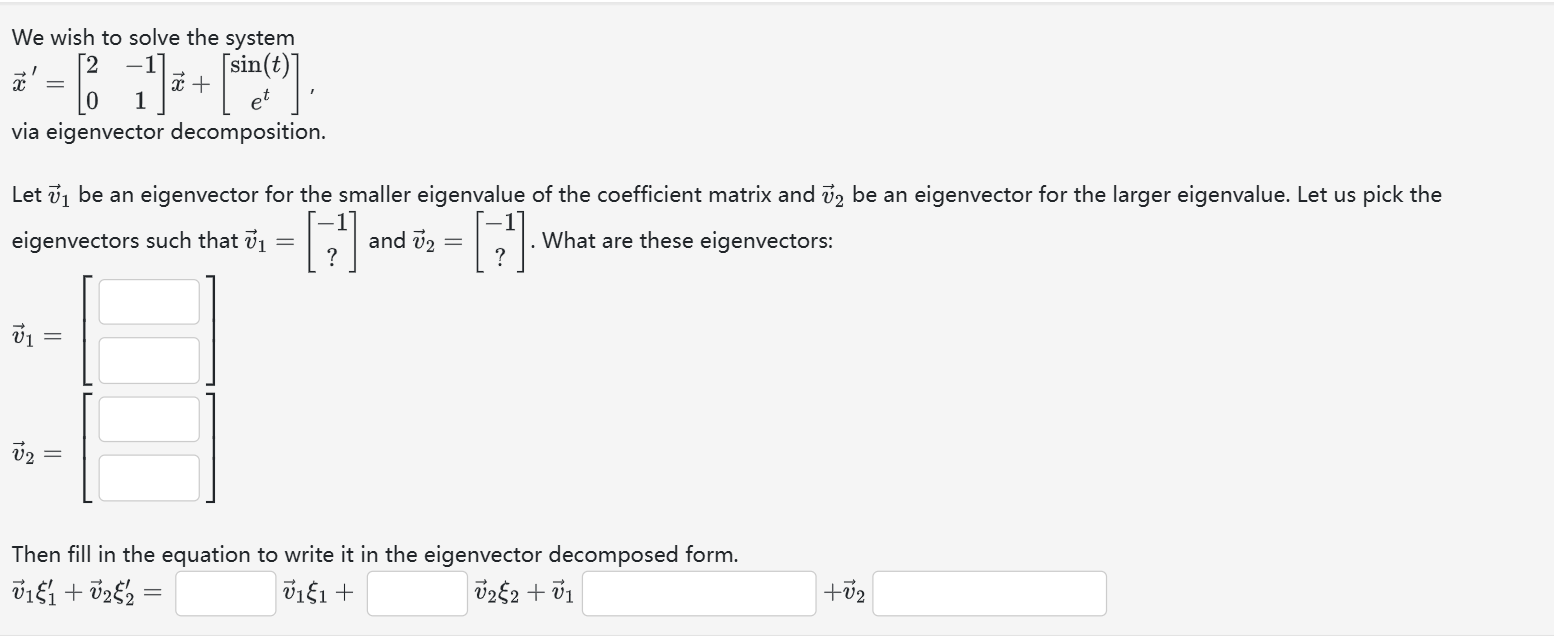
We wish to solve the system
vec(x)^(')=[[2,-1],[0,1]]vec(x)+[[sin(t)],[e^(t)]]
via eigenvector decomposition.
Let vec(v)_(1) be an eigenvector for the smaller eigenvalue of the coefficient matrix and vec(v)_(2) be an eigenvector for the larger eigenvalue. Let us pick the
eigenvectors such that vec(v)_(1)=[[-1],[?]] and vec(v)_(2)=[[-1],[?]]. What are these eigenvectors:
Then fill in the equation to write it in the eigenvector decomposed form.
vec(v)_(1)\xi _(1)^(')+vec(v)_(2)\xi _(2)^(')=,vec(v)_(1)\xi _(1)+,vec(v)_(2)\xi _(2)+vec(v)_(1)+vec(v)_(2)