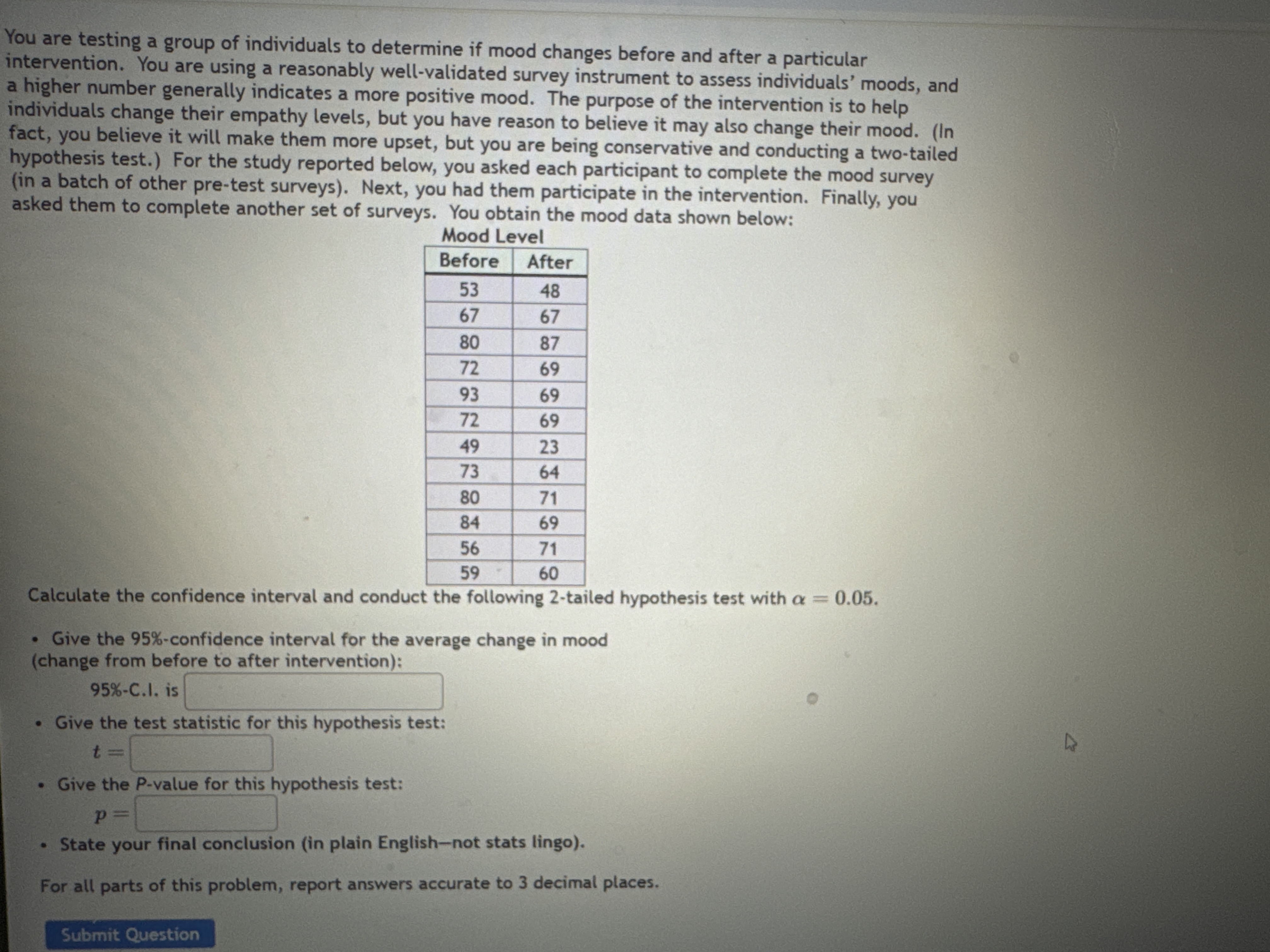
(Solved): You are testing a group of individuals to determine if mood changes before and after a particular in ...

You are testing a group of individuals to determine if mood changes before and after a particular intervention. You are using a reasonably well-validated survey instrument to assess individuals' moods, and a higher number generally indicates a more positive mood. The purpose of the intervention is to help individuals change their empathy levels, but you have reason to believe it may also change their mood. (In fact, you believe it will make them more upset, but you are being conservative and conducting a two-tailed hypothesis test.) For the study reported below, you asked each participant to complete the mood survey (in a batch of other pre-test surveys). Next, you had them participate in the intervention. Finally, you asked them to complete another set of surveys. You obtain the mood data shown below: Mood Level Calculate the confidence interval and conduct the following 2-tailed hypothesis test with \( \alpha=0.05 \). - Give the \( 95 \% \)-confidence interval for the average change in mood (change from before to after intervention): \[ 95 \% \text {-C.I. is } \] - Give the test statistic for this hypothesis test: \[ t= \] - Give the \( P \)-value for this hypothesis test: \[ p= \] - State your final conclusion (in plain English-not stats lingo). For all parts of this problem, report answers accurate to 3 decimal places.